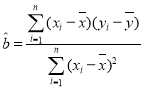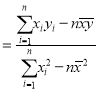题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性.
的单调性.
(2)试问是否存在![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)见解析;(2) 存在;![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)![]() ,
,![]() ,
,
所以![]() 得
得![]() ,所以通过对
,所以通过对![]() 与
与![]() 的大小关系进行分类讨论得
的大小关系进行分类讨论得![]() 的单调性;
的单调性;
(2)假设存在满足题意的![]() 的值,由题意需
的值,由题意需![]() ,所以由(1)的单调性求
,所以由(1)的单调性求![]() 即可;
即可;
又因为![]() 对
对![]() 恒成立,所以可以考虑从区间
恒成立,所以可以考虑从区间![]() 内任取一个
内任取一个![]() 值代入,解出
值代入,解出![]() 的取值范围,从而将
的取值范围,从而将![]() 的范围缩小减少讨论.
的范围缩小减少讨论.
解:(1)![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.
上单调递增.
(2)假设存在![]() ,使得
,使得![]() 对
对![]() 恒成立.
恒成立.
则![]() ,即
,即![]() ,
,
设![]() ,则存在
,则存在![]() ,使得
,使得![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以
,所以![]() 时
时![]() 即
即![]() .
.
又因为![]() 对
对![]() 恒成立时,需
恒成立时,需![]() ,
,
所以由(1)得:
当![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
且![]() 成立,从而
成立,从而![]() 满足题意.
满足题意.
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增,
上单调递增,
所以
所以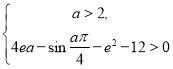 (*)
(*)
设![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,
所以![]() 的零点小于2,从而不等式组(*)的解集为
的零点小于2,从而不等式组(*)的解集为![]() ,
,
所以![]() 即
即![]() .
.
综上,存在![]() ,使得
,使得![]() 对
对![]() 恒成立,且
恒成立,且![]() 的取值范围为
的取值范围为![]() .
.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
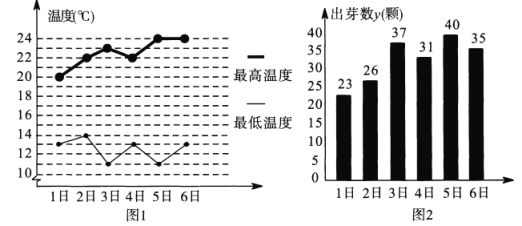
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】某地级市共有![]() 中小学生,其中有
中小学生,其中有![]() 学生在
学生在![]() 年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为
年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为![]() ,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助
,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助![]() 元、
元、![]() 元、
元、![]() 元,经济学家调查发现,当地人均可支配年收入较上一年每增加
元,经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有![]() 转为一般困难,特别困难的学生中有
转为一般困难,特别困难的学生中有![]() 转为很困难.现统计了该地级市
转为很困难.现统计了该地级市![]() 年到
年到![]() 年共
年共![]() 年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取
取![]() 时代表
时代表![]() 年,
年,![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.(
为常数.(![]() 年至
年至![]() 年该市中学生人数大致保持不变)
年该市中学生人数大致保持不变)
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() ,
,![]()
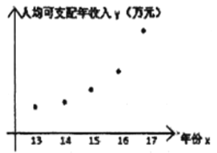
(1)估计该市![]() 年人均可支配年收入;
年人均可支配年收入;
(2)求该市![]() 年的“专项教育基金”的财政预算大约为多少?
年的“专项教育基金”的财政预算大约为多少?
附:对于一组具有线性相关关系的数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为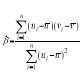 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.
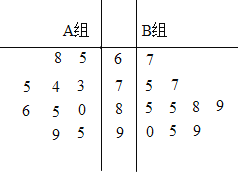
(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: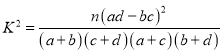 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|