题目内容
9.一个几何体的三视图如图所示,其中左视图为直角三角形,则该几何体的体积为( )
| A. | 16$\sqrt{2}$ | B. | $\frac{{4\sqrt{2}}}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $\frac{{16\sqrt{2}}}{3}$ |
分析 根据几何体的三视图,得出该几何体是一侧面垂直于底面的三棱锥,画出直观图,根据数据求出体积.
解答 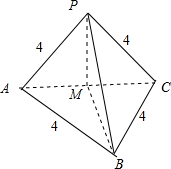 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是侧面PAC⊥底面ABC的三棱锥,如图所示;
过点P作PM⊥AC,交AC与点M,连接BM,
则PM⊥平面ABC,且PM=2$\sqrt{2}$,
∴BM⊥AC,且BM=2$\sqrt{2}$,
∴AC=2AM=2$\sqrt{{4}^{2}{-(2\sqrt{2})}^{2}}$=4$\sqrt{2}$;
∴三棱锥的体积为
V三棱锥P-ABC=$\frac{1}{3}$×$\frac{1}{2}$×4$\sqrt{2}$×2$\sqrt{2}$×2$\sqrt{2}$=$\frac{16\sqrt{2}}{3}$.
故选:D.
点评 本题考查了利用几何体的三视图求体积的应用问题,是基础题目.

练习册系列答案
相关题目
19.若集合P={y|y≥0},且P∪Q=Q,则集合Q可能是( )
| A. | {y|y=x2+1} | B. | {y|y=2x} | C. | {y|y=lgx} | D. | ∅ |
4.设函数f(x)=$\frac{1}{2}$cosωx对任意的x∈R,都有f($\frac{π}{6}$-x)=f($\frac{π}{6}$+x),若函数g(x)=-2+3sinωx,则g($\frac{π}{6}$)的值是( )
| A. | 1 | B. | -5或3 | C. | -2 | D. | $\frac{1}{2}$ |
18.用辗转相除法求294和84的最大公约数,则所求最大公约数为 ( )
| A. | 21 | B. | 42 | C. | 84 | D. | 168 |
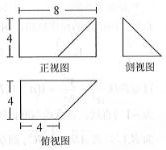 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.