题目内容
4.已知互不相等的正数a,b,c,d,p,q满足a,c,b,d成等差数列,a,p,b,q成等比数列,则( )| A. | c<p,d>q | B. | c>p,d>q | C. | c>p,d<q | D. | c<p,d<q |
分析 设公差为n,公比为m,且n≠0、m>0、m≠1,由等差、等比数列的通项公式分别求出c、b、d、p、q,建立n、m的关系式,利用作差法比较出c和p的大小,化简d-q后构造函数f(m),求出此函数的导数,判断出函数的单调性、求出最大值,即可判断出d和q大小关系.
解答 解:设公差为n,公比为m,且n≠0、m>0、m≠1,
则c=a+n、b=a+2n、d=a+3n,p=am、b=am2、q=am3,
所以a+2n=am2,得n=$\frac{1}{2}(a{m}^{2}-a)$,
所以c-p=a+n-am=a+$\frac{1}{2}(a{m}^{2}-a)$-am=$\frac{1}{2}a({m}^{2}-2m+1)$=$\frac{1}{2}a({m-1)}^{2}$>0,
则c-p>0,即c>p,
d-q=a+3n-am3=a+$\frac{3}{2}(a{m}^{2}-a)$-am2=$\frac{3}{2}a({-2m}^{3}+3{m}^{2}-1)$,
设f(m)=-2m3+3m2-1,则f′(m)=-6m2+6m,
因为m>0、m≠1,所以当0<m<1时,f′(m)>0,当m>1时,f′(m)<0,
所以函数f(m)在(0,1)上递增,在(1,+∞)上递减,
则f(m) 的最大值是f(1)=0,即f(m)<f(1)=0,
综上可得,d-q<0,则d<q,
故选:C.
点评 本题考查了等差、等比数列的通项公式,导数与函数的单调性、最值的关系,以及作差法、构造函数法的综合应用,考查化简、变形能力.

练习册系列答案
相关题目
9.已知复数z=(1-i)(1+2i),其中i为虚数单位,则$\overline{z}$的虚部为( )
| A. | -i | B. | 1 | C. | -1 | D. | i |
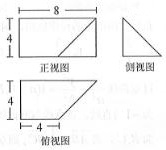 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.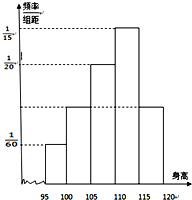 某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率
某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率