题目内容
设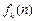 为关于n的k
为关于n的k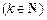 次多项式.数列{an}的首项
次多项式.数列{an}的首项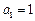 ,前n项和为
,前n项和为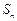 .对于任意的正整数n,
.对于任意的正整数n,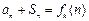 都成立.
都成立.
(1)若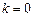 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;
(2)试确定所有的自然数k,使得数列{an}能成等差数列
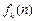 为关于n的k
为关于n的k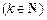 次多项式.数列{an}的首项
次多项式.数列{an}的首项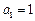 ,前n项和为
,前n项和为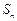 .对于任意的正整数n,
.对于任意的正整数n,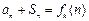 都成立.
都成立.(1)若
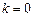 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;(2)试确定所有的自然数k,使得数列{an}能成等差数列
(1)若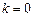 ,则
,则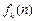 即
即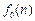 为常数,不妨设
为常数,不妨设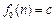 (c为常数).
(c为常数).
因为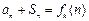 恒成立,所以
恒成立,所以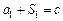 ,即
,即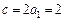 .
.
而且当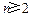 时,
时,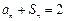 , ①
, ①
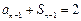 , ②
, ②
①-②得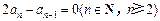 .
.
若an=0,则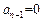 ,…,a1=0,与已知矛盾,所以
,…,a1=0,与已知矛盾,所以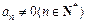 .
.
故数列{an}是首项为1,公比为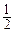 的等比数列.
的等比数列.
【解】(2)(i) 若k=0,由(1)知,不符题意,舍去.
(ii) 若k=1,设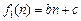 (b,c为常数),
(b,c为常数),
当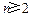 时,
时,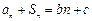 , ③
, ③
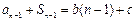 , ④
, ④
③-④得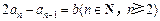 .
.
要使数列{an}是公差为d(d为常数)的等差数列,必须有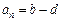 (常数),
(常数),
而a1=1,故{an}只能是常数数列,通项公式为an =1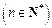 ,
,
故当k=1时,数列{an}能成等差数列,其通项公式为an =1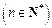 ,此时
,此时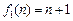 .
.
(iii) 若k=2,设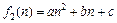 (
(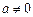 ,a,b,c是常数),
,a,b,c是常数),
当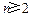 时,
时,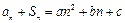 , ⑤
, ⑤
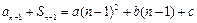 , ⑥
, ⑥
⑤-⑥得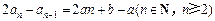 ,要使数列{an}是公差为d(d为常数)的等差数列,必须有
,要使数列{an}是公差为d(d为常数)的等差数列,必须有
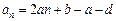 ,且d=2a,
,且d=2a,
考虑到a1=1,所以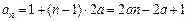
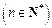 .
.
故当k=2时,数列{an}能成等差数列,其通项公式为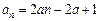
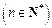 ,
,
此时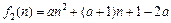 (a为非零常数). (iv) 当
(a为非零常数). (iv) 当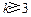 时,若数列{an}能成等差数列,则
时,若数列{an}能成等差数列,则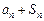 的表达式中n的最高次数为2,故数列{an}
的表达式中n的最高次数为2,故数列{an}
不能成等差数列.
综上得,当且仅当k=1或2时,数列{an}能成等差数列.
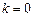 ,则
,则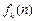 即
即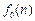 为常数,不妨设
为常数,不妨设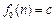 (c为常数).
(c为常数).因为
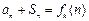 恒成立,所以
恒成立,所以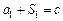 ,即
,即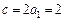 .
.而且当
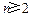 时,
时,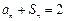 , ①
, ①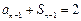 , ②
, ②①-②得
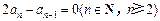 .
.若an=0,则
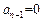 ,…,a1=0,与已知矛盾,所以
,…,a1=0,与已知矛盾,所以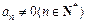 .
.故数列{an}是首项为1,公比为
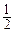 的等比数列.
的等比数列. 【解】(2)(i) 若k=0,由(1)知,不符题意,舍去.
(ii) 若k=1,设
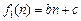 (b,c为常数),
(b,c为常数),当
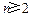 时,
时,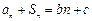 , ③
, ③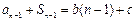 , ④
, ④③-④得
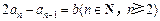 .
.要使数列{an}是公差为d(d为常数)的等差数列,必须有
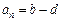 (常数),
(常数),而a1=1,故{an}只能是常数数列,通项公式为an =1
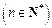 ,
,故当k=1时,数列{an}能成等差数列,其通项公式为an =1
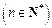 ,此时
,此时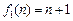 .
.(iii) 若k=2,设
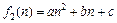 (
(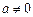 ,a,b,c是常数),
,a,b,c是常数),当
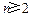 时,
时,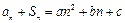 , ⑤
, ⑤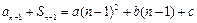 , ⑥
, ⑥⑤-⑥得
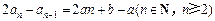 ,要使数列{an}是公差为d(d为常数)的等差数列,必须有
,要使数列{an}是公差为d(d为常数)的等差数列,必须有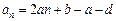 ,且d=2a,
,且d=2a,考虑到a1=1,所以
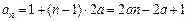
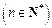 .
.故当k=2时,数列{an}能成等差数列,其通项公式为
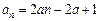
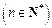 ,
,此时
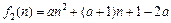 (a为非零常数). (iv) 当
(a为非零常数). (iv) 当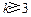 时,若数列{an}能成等差数列,则
时,若数列{an}能成等差数列,则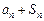 的表达式中n的最高次数为2,故数列{an}
的表达式中n的最高次数为2,故数列{an}不能成等差数列.
综上得,当且仅当k=1或2时,数列{an}能成等差数列.
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
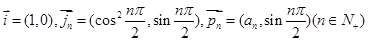 ,数列
,数列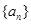 满足:
满足: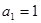 ,
,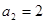 ,
,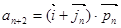 .
.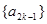 是等差数列;数列
是等差数列;数列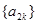 是等比数列;(其中
是等比数列;(其中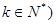 ;
;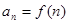 ,对任意的正整数
,对任意的正整数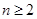 ,不等式
,不等式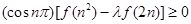 恒成立,求
恒成立,求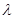 的取值范围.
的取值范围.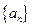 的前
的前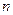 项的和
项的和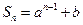 ,
,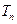 为数列
为数列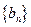 的前
的前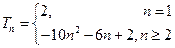 .
.
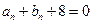 的自然数
的自然数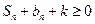 对于任意的
对于任意的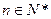 ,
,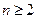 恒成立,求实数
恒成立,求实数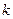 的最小值,并求出此时相应的
的最小值,并求出此时相应的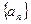 为等差数列,且
为等差数列,且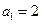 ,
,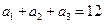 .
.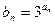 ,求证:数列
,求证:数列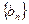 是等比数列;
是等比数列;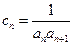 ,求数列
,求数列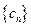 的前
的前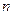 项和
项和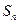 .
.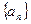 中,
中,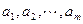 是首项为
是首项为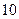 ,公差为
,公差为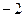 的等差数列;
的等差数列;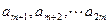 是首项为
是首项为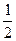 ,公比为
,公比为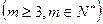 ,并对任意
,并对任意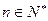 ,均有
,均有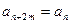 成立,(1)当
成立,(1)当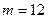 时,求
时,求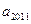 ; (2)若
; (2)若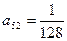 ,试求
,试求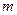 的值;(3)判断是否存在
的值;(3)判断是否存在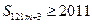 成立,若存在,求出
成立,若存在,求出 ,点An(n, Sn)在函数y="f(x)" (n∈N*)的图像上 ,
,点An(n, Sn)在函数y="f(x)" (n∈N*)的图像上 ,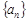 为等差数列; (2)设
为等差数列; (2)设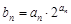 ,求数列
,求数列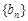 的前
的前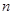 项和
项和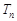
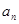 }的前n项和为
}的前n项和为 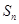 ,若
,若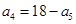 ,则
,则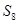 =( )
=( )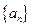 的前
的前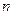 项和为
项和为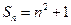 ,数列
,数列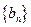 满足:
满足: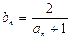 ,前
,前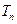 ,设
,设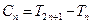 。 (1)求数列
。 (1)求数列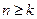 时,总有
时,总有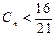 成立,若存在,求自然数
成立,若存在,求自然数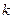 的最小值。若不存在,说明理由。
的最小值。若不存在,说明理由。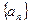 满足
满足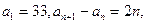 则
则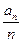 的最小值为
的最小值为