题目内容
(本小题满分12分)
已知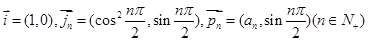 ,数列
,数列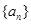 满足:
满足: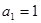 ,
,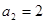 ,
,
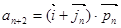 .
.
(Ⅰ) 求证:数列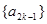 是等差数列;数列
是等差数列;数列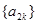 是等比数列;(其中
是等比数列;(其中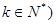 ;
;
(Ⅱ) 记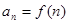 ,对任意的正整数
,对任意的正整数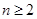 ,不等式
,不等式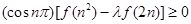 恒成立,求
恒成立,求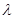 的取值范围.
的取值范围.
已知
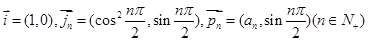 ,数列
,数列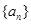 满足:
满足: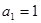 ,
,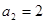 ,
,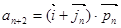 .
.(Ⅰ) 求证:数列
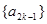 是等差数列;数列
是等差数列;数列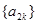 是等比数列;(其中
是等比数列;(其中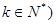 ;
;(Ⅱ) 记
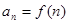 ,对任意的正整数
,对任意的正整数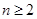 ,不等式
,不等式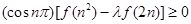 恒成立,求
恒成立,求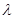 的取值范围.
的取值范围.解:
(Ⅰ)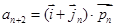
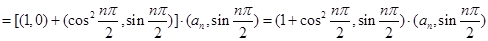
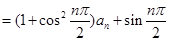 ,…………2分
,…………2分
当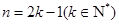 时,
时,
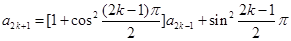
=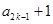 ,即
,即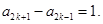
所以数列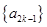 是首项为1、公差为1的等差数列,…………4分
是首项为1、公差为1的等差数列,…………4分
当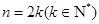 时,
时,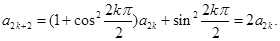
所以数列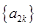 是首项为2、公比为2的等比数列,…………6分
是首项为2、公比为2的等比数列,…………6分
(Ⅱ)由(Ⅰ)可知: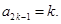
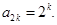
故数列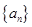 的通项公式为
的通项公式为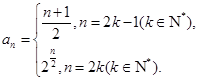 …………7分
…………7分
当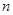 为奇数时,
为奇数时,
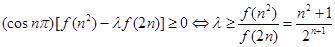
令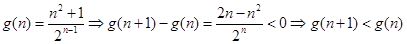
所以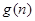 为单调递减函数,
为单调递减函数,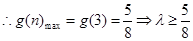 …………10分
…………10分
当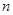 为偶数时,
为偶数时,
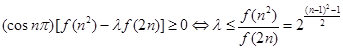
令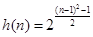 ,显然
,显然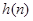 为单调递增函数,
为单调递增函数,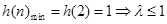
综上: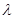 的取值围是
的取值围是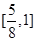 …………12分
…………12分
(Ⅰ)
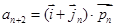
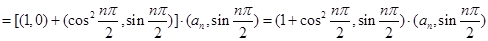
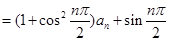 ,…………2分
,…………2分当
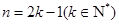 时,
时,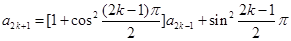
=
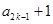 ,即
,即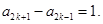
所以数列
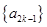 是首项为1、公差为1的等差数列,…………4分
是首项为1、公差为1的等差数列,…………4分当
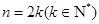 时,
时,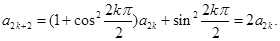
所以数列
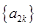 是首项为2、公比为2的等比数列,…………6分
是首项为2、公比为2的等比数列,…………6分(Ⅱ)由(Ⅰ)可知:
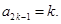
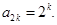
故数列
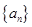 的通项公式为
的通项公式为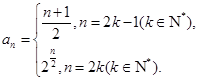 …………7分
…………7分当
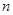 为奇数时,
为奇数时,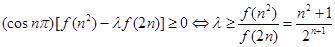
令
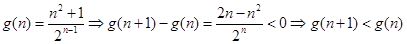
所以
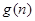 为单调递减函数,
为单调递减函数,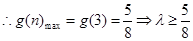 …………10分
…………10分当
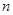 为偶数时,
为偶数时,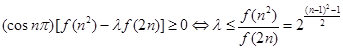
令
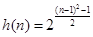 ,显然
,显然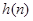 为单调递增函数,
为单调递增函数,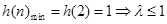
综上:
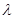 的取值围是
的取值围是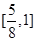 …………12分
…………12分略

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
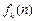 为关于n的k
为关于n的k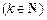 次多项式.数列{an}的首项
次多项式.数列{an}的首项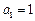 ,前n项和为
,前n项和为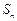 .对于任意的正整数n,
.对于任意的正整数n,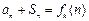 都成立.
都成立.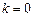 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;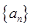 中,
中,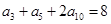 ,则此数列的前
,则此数列的前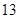 项的和等于
项的和等于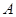 、
、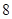
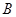 、
、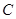 、
、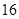
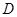 、
、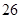
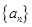 的前
的前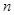 项和为
项和为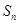 ,若
,若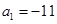 ,
,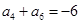 ,则当
,则当 ,
, =5,
=5, =10,则
=10,则 =:
=:



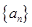 中,公差为
中,公差为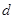 ,且
,且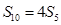 ,则
,则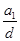 等于 ( )
等于 ( )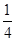
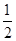
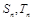 ,若
,若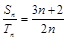 ,则
,则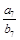 =( )
=( )



 中,
中, 则
则 ( )
( )


