题目内容
(本小题16分)如图所示,数列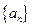 的前
的前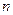 项的和
项的和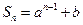 ,
,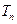 为数列
为数列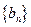 的前
的前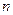 项的和,且
项的和,且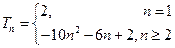 .
.

(1)求数列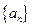 、
、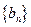 的通项公式;
的通项公式;
(2)找出所有满足: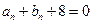 的自然数
的自然数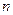 的值(不必证明);
的值(不必证明);
(3)若不等式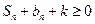 对于任意的
对于任意的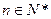 ,
,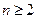 恒成立,求实数
恒成立,求实数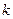 的最小值,并求出此时相应的
的最小值,并求出此时相应的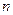 的值.
的值.
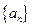 的前
的前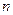 项的和
项的和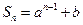 ,
,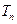 为数列
为数列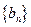 的前
的前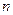 项的和,且
项的和,且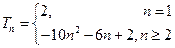 .
.
(1)求数列
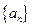 、
、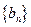 的通项公式;
的通项公式;(2)找出所有满足:
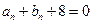 的自然数
的自然数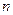 的值(不必证明);
的值(不必证明);(3)若不等式
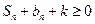 对于任意的
对于任意的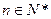 ,
,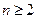 恒成立,求实数
恒成立,求实数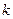 的最小值,并求出此时相应的
的最小值,并求出此时相应的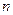 的值.
的值.解:(1)由题意得: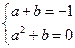 ,解之得:
,解之得: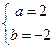 ,
,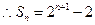
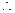 当
当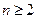 时,
时,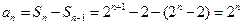
当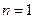 时,
时,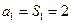 符合上式,故
符合上式,故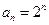 ,
,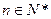 . -----------------------------2
. -----------------------------2
当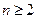 时,
时,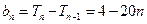
当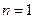 时,
时,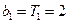 不符合上式,故
不符合上式,故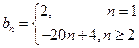 . -------------------------4
. -------------------------4
(2)当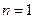 时,
时,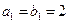 ,且
,且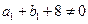 ,不合
,不合
当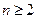 时,由题意可得:
时,由题意可得: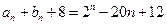
而方程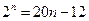 只有
只有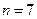 满足条件,故当
满足条件,故当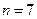 时,
时,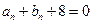 -------------------8
-------------------8
(3)由题得:
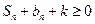 ,
,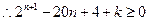 对于一切
对于一切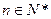 ,
,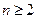 恒成立
恒成立
即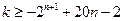 。。。。。。。。。。10
。。。。。。。。。。10
令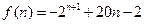 (
(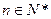 ,
,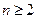 )
)
则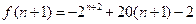
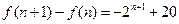 ------------------------12
------------------------12
当 时,
时,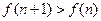 ;当
;当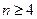 时,
时,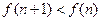
而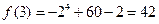 ,
,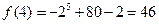
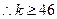
故当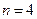 时,
时,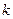 的最小值为46. ----------------------------16
的最小值为46. ----------------------------16
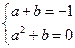 ,解之得:
,解之得: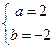 ,
,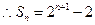
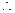 当
当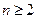 时,
时,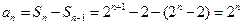
当
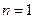 时,
时,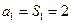 符合上式,故
符合上式,故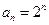 ,
,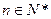 . -----------------------------2
. -----------------------------2当
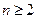 时,
时,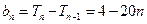
当
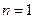 时,
时,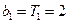 不符合上式,故
不符合上式,故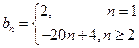 . -------------------------4
. -------------------------4(2)当
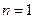 时,
时,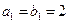 ,且
,且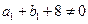 ,不合
,不合当
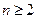 时,由题意可得:
时,由题意可得: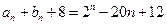
而方程
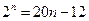 只有
只有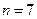 满足条件,故当
满足条件,故当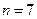 时,
时,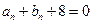 -------------------8
-------------------8(3)由题得:
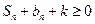 ,
,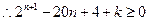 对于一切
对于一切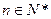 ,
,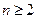 恒成立
恒成立即
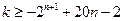 。。。。。。。。。。10
。。。。。。。。。。10令
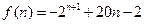 (
(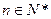 ,
,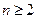 )
)则
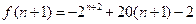
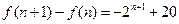 ------------------------12
------------------------12当
 时,
时,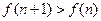 ;当
;当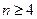 时,
时,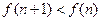
而
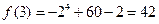 ,
,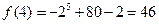
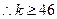
故当
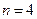 时,
时,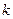 的最小值为46. ----------------------------16
的最小值为46. ----------------------------16略

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
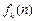 为关于n的k
为关于n的k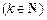 次多项式.数列{an}的首项
次多项式.数列{an}的首项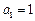 ,前n项和为
,前n项和为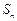 .对于任意的正整数n,
.对于任意的正整数n,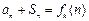 都成立.
都成立.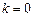 ,求证:数列{an}是等比数列;
,求证:数列{an}是等比数列;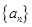 的前
的前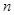 项和为
项和为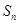 ,若
,若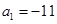 ,
,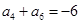 ,则当
,则当 ,
, =5,
=5, =10,则
=10,则 =:
=:



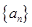 中,公差为
中,公差为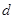 ,且
,且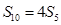 ,则
,则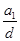 等于 ( )
等于 ( )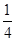
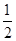
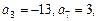 其前
其前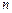 项和为
项和为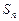 ,求
,求 前17项和
前17项和 ,则
,则
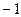 ,
,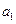 ,
,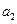 ,
,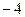 成等差数列,
成等差数列,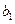 ,
,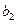 ,
,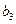 ,
,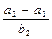 的值为___________________
的值为___________________