Question

【题目】已知抛物线的顶点在原点，对称轴为坐标轴，它与双曲线：交于点，抛物线的准线过双曲线的左焦点.

（1）求抛物线与双曲线的标准方程；

（2）若斜率为的直线过点且与抛物线只有一个公共点，求直线的方程.

Answer 1

【答案】（1）抛物线方程为;双曲线的方程为.（2）直线的方程为或

【解析】

（1）根据抛物线的准线过双曲线的左焦点,可知抛物线开口向右,则设抛物线方程为,代入即可求得抛物线方程;由抛物线方程可得抛物线的准线方程,进而得双曲线的,由双曲线中的关系及代入,解方程可求得,即可得双曲线的标准方程.

（2）讨论直线的斜率和两种情况:当时一定成立,由所过定点坐标可得直线方程;当时,联立直线与抛物线方程,由判别式即可求得斜率,再由点斜式可得直线方程.

（1）因为抛物线的准线过双曲线的左焦点,

设抛物线方程为

由抛物线过,代入可得

解得,所以抛物线方程为

抛物线的准线方程为,所以双曲线的

同时将代入双曲线方程,即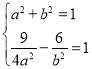 解方程组可得

所以双曲线的标准方程为

（2）斜率为的直线过点且与抛物线只有一个公共点

当时,直线方程为,满足题意

当时,直线可设为

则,化简可得

由与直线抛物线只有一个公共点

可得

解得,所以直线的方程为

综上可得直线的方程为或