题目内容
【题目】甲与乙午觉醒来后，发现自己的手表因故停止转动，于是他们想借助收音机，利用电台整点报时确认时间．
(1)求甲等待的时间不多于10分钟的概率；
(2)求甲比乙多等待10分钟以上的概率．
【答案】(1) 
(2)
【解析】
（1）直接由几何概型中的长度型概率计算公式求解。
（2）设甲需要等待的时间为
，乙需要等待的时间为
，由已知列不等式组，利用几何概型中的面积型概率计算公式求解。
解：（1）因为电台每隔1小时报时一次，
甲在
之间任何一个时刻打开收音机是等可能的，
所以他在哪个时间段打开收音机的概率只与该时间段的长度有关，
而与该时间段的位置无关，符合几何概型的条件.
设事件
为“甲等待的时间不多于10分钟”，
则事件恰好是打开收音机的时刻位于
时间段内，
因此由几何概型的概率公式得
，
所以“甲等待的时间不多于10分钟“的概率为.
（2）因为甲、乙两人起床的时间是任意的，
所以所求事件是一个与两个变量相关的几何概型，且为面积型.
设甲需要等待的时间为，乙需要等待的时间为（10分钟为一个长度单位）.
则由已知可得，对应的基本事件空间为
.
甲比乙多等待10分钟以上对应的事件为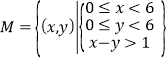
.
在平面直角坐标系中作出两个不等式组所表示的平面区域，如图所示.
显然
表示一个边长为6的正方形
的内部及线段
，
，
其面积
.
表示的是腰长为5的等腰直角三角形
的内部及线段
，
其面积
，故所求事件的概率为
.
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
【题目】某大型水果超市每天以
元/千克的价格从水果基地购进若干
水果，然后以
元/千克的价格出售，若有剩余，则将剩下的水果以
元/千克的价格退回水果基地，为了确定进货数量，该超市记录了水果最近
天的日需求量（单位：千克），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以天记录的各日需求量的频率代替各日需求量的概率.
（1）求该超市水果日需求量
（单位：千克）的分布列；
（2）若该超市一天购进水果
千克，记超市当天水果获得的利润为
（单位：元），求的分布列及其数学期望.
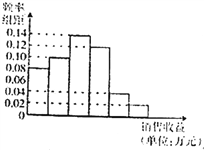
【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入
万元广告费用，并将各地的销售收益（单位：万元）绘制成如图所示的频率分布直方图.由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从
开始计数的.
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 5 | 7 |
（Ⅰ）根据频率分布直方图计算图中各小长方形的宽度；
（Ⅱ）该公司按照类似的研究方法，测得另外一些数据，并整理得到上表：
表中的数据显示
与
之间存在线性相关关系，求关于的回归方程；
（Ⅲ）若广告投入
万元时，实际销售收益为
万元，求残差
.
附：
，
