题目内容
已知{an}是等差数列,a1=2,a2=3,若在每相邻两项之间插入3个数,使它和原数列的数构成一个新的等差数列,
(1)原数列的第12项是新数列的第几项?
(2)新数列的第29项是原数列的第几项?
(1)原数列的第12项是新数列的第几项?
(2)新数列的第29项是原数列的第几项?
(1)原数列的第12项是新数列的第45项.
(2)新数列的第29项是原数列的第8项.
(2)新数列的第29项是原数列的第8项.
数列的通项公式是研究数列问题的重要工具.能否由条件找到两个数列的通项公式是解决此题的关键.
∵数列{an}中a1=2,d=a2-a1=3-2=1,
∴an=a1+(n-1)d=2+(n-1)×1=n+1.
设新数列为{bn},公差为d′,据题意知b1=2,b5=3,
则d′=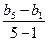 =
=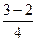 =
=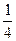 ,
,
∴bn=2+(n-1)×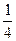 =
=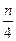 +
+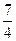 .
.
(1)a12=12+1=13,令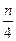 +
+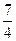 =13,得n=45,故原数列的第12项是新数列的第45项.
=13,得n=45,故原数列的第12项是新数列的第45项.
(2)b29=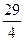 +
+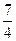 =9,令n+1=9,得n=8,故新数列的第29项是原数列的第8项.
=9,令n+1=9,得n=8,故新数列的第29项是原数列的第8项.
∵数列{an}中a1=2,d=a2-a1=3-2=1,
∴an=a1+(n-1)d=2+(n-1)×1=n+1.
设新数列为{bn},公差为d′,据题意知b1=2,b5=3,
则d′=
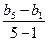 =
=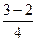 =
=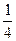 ,
,∴bn=2+(n-1)×
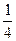 =
=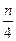 +
+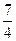 .
.(1)a12=12+1=13,令
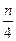 +
+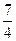 =13,得n=45,故原数列的第12项是新数列的第45项.
=13,得n=45,故原数列的第12项是新数列的第45项.(2)b29=
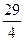 +
+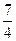 =9,令n+1=9,得n=8,故新数列的第29项是原数列的第8项.
=9,令n+1=9,得n=8,故新数列的第29项是原数列的第8项.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 满足条件:
满足条件: ,且
,且 )
)
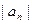 满足:
满足: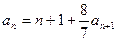 ,且存在大于1的整数k使
,且存在大于1的整数k使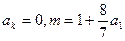 。
。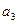 表示m(不必化简)
表示m(不必化简)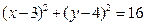 ,直线
,直线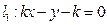 .
.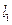 与圆交于两个不同点
与圆交于两个不同点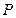 、
、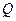 ,求实数
,求实数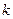 的取值范围;
的取值范围;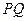 的中点为
的中点为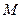 ,
,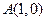 ,且
,且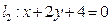 的交点为
的交点为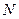 ,求证:
,求证: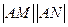 为定值
为定值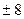 D
D