题目内容
在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,求当n取何值时,Sn取得最大值,并求出它的最大值.
当n=12或13时,Sn取得最大值,且最大值为S12= 130.
方法一 ∵a1=20,S10=S15,
∴10×20+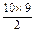 d=15×20+
d=15×20+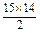 d,
d,
∴d=- . 4分
. 4分
∴an=20+(n-1)×(- )=-
)=- n+
n+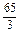 . 8分
. 8分
∴a13="0. " 10分
即当n≤12时,an>0,n≥14时,an<0.
∴当n=12或13时,Sn取得最大值,且最大值为
S12=S13=12×20+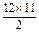
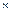 (-
(- )="130. " 14分
)="130. " 14分
方法二 同方法一求得d=- . 4分
. 4分
∴Sn=20n+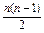 ·(-
·(- )
)
=-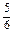 n2+
n2+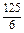 n
n
=-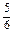
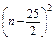 +
+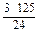 . 8分
. 8分
∵n∈N+,∴当n=12或13时,Sn有最大值,
且最大值为S12=S13="130. " 14分
方法三 同方法一得d=- . 4分
. 4分
又由S10=S15,得a11+a12+a13+a14+a15="0. " 8分
∴5a13=0,即a13="0. " 10分
∴当n=12或13时,Sn有最大值,
且最大值为S12=S13="130. " 14分
∴10×20+
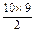 d=15×20+
d=15×20+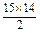 d,
d,∴d=-
 . 4分
. 4分∴an=20+(n-1)×(-
 )=-
)=- n+
n+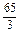 . 8分
. 8分∴a13="0. " 10分
即当n≤12时,an>0,n≥14时,an<0.
∴当n=12或13时,Sn取得最大值,且最大值为
S12=S13=12×20+
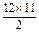
 (-
(- )="130. " 14分
)="130. " 14分方法二 同方法一求得d=-
 . 4分
. 4分∴Sn=20n+
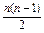 ·(-
·(- )
)=-
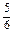 n2+
n2+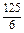 n
n=-
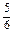
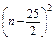 +
+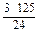 . 8分
. 8分∵n∈N+,∴当n=12或13时,Sn有最大值,
且最大值为S12=S13="130. " 14分
方法三 同方法一得d=-
 . 4分
. 4分又由S10=S15,得a11+a12+a13+a14+a15="0. " 8分
∴5a13=0,即a13="0. " 10分
∴当n=12或13时,Sn有最大值,
且最大值为S12=S13="130. " 14分

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 ,an=2-
,an=2-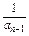 (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).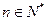 ,不等式
,不等式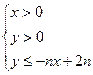 所表示的平面区域为
所表示的平面区域为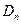 ,把
,把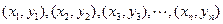
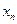 ,
,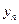 ;
;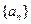 满足
满足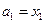 ,且
,且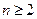 时
时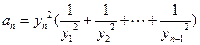 .证明当
.证明当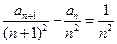 ;
;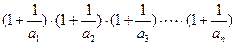 与4的大小关系.
与4的大小关系.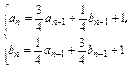 (n≥2).
(n≥2).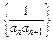 的前n项和Tn.
的前n项和Tn.



 中,
中, ,则
,则 ( )
( )

