题目内容
已知椭圆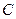 的对称轴为坐标轴,一个焦点为
的对称轴为坐标轴,一个焦点为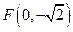 ,点
,点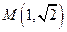 在椭圆
在椭圆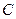 上
上
(Ⅰ)求椭圆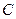 的谢方程
的谢方程
(Ⅱ)已知直线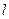 :
: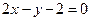 与椭圆
与椭圆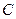 交于
交于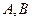 两点,求
两点,求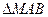 的面积
的面积
(Ⅲ)设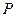 为椭圆
为椭圆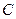 上一点,若
上一点,若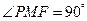 ,求
,求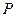 点的坐标
点的坐标
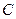 的对称轴为坐标轴,一个焦点为
的对称轴为坐标轴,一个焦点为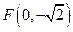 ,点
,点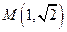 在椭圆
在椭圆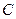 上
上(Ⅰ)求椭圆
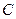 的谢方程
的谢方程(Ⅱ)已知直线
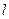 :
: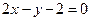 与椭圆
与椭圆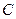 交于
交于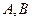 两点,求
两点,求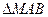 的面积
的面积(Ⅲ)设
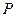 为椭圆
为椭圆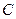 上一点,若
上一点,若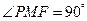 ,求
,求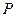 点的坐标
点的坐标


略

练习册系列答案
相关题目
题目内容
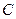 的对称轴为坐标轴,一个焦点为
的对称轴为坐标轴,一个焦点为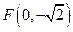 ,点
,点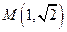 在椭圆
在椭圆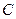 上
上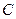 的谢方程
的谢方程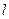 :
: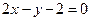 与椭圆
与椭圆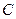 交于
交于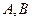 两点,求
两点,求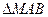 的面积
的面积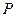 为椭圆
为椭圆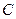 上一点,若
上一点,若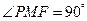 ,求
,求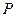 点的坐标
点的坐标


