题目内容
已知定义域为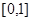 的函数
的函数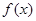 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的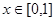 ,总有
,总有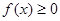 ;
;
②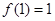 ;
;
③当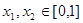 ,且
,且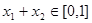 时,
时,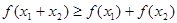 成立.
成立.
称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知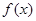 为“友谊函数”,求
为“友谊函数”,求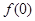 的值;
的值;
(2)函数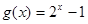 在区间
在区间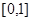 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;
(3)已知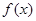 为“友谊函数”,假定存在
为“友谊函数”,假定存在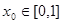 ,使得
,使得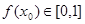 ,且
,且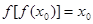 ,求证:
,求证: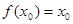 .
.
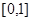 的函数
的函数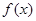 同时满足以下三个条件:
同时满足以下三个条件:①对任意的
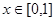 ,总有
,总有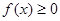 ;
;②
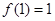 ;
; ③当
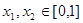 ,且
,且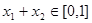 时,
时,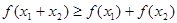 成立.
成立.称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知
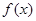 为“友谊函数”,求
为“友谊函数”,求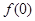 的值;
的值;(2)函数
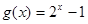 在区间
在区间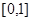 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;(3)已知
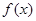 为“友谊函数”,假定存在
为“友谊函数”,假定存在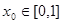 ,使得
,使得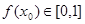 ,且
,且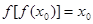 ,求证:
,求证: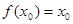 .
.(1)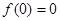 ;(2)
;(2)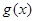 在
在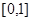 上为友谊函数;(3)证明过程见解析.
上为友谊函数;(3)证明过程见解析.
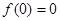 ;(2)
;(2)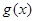 在
在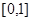 上为友谊函数;(3)证明过程见解析.
上为友谊函数;(3)证明过程见解析.试题分析:(1)赋值可考虑取
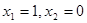 ,代入
,代入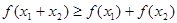 ,可得
,可得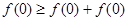 ,由已知
,由已知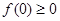 ,可得
,可得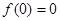 .
.(2)要判断函数
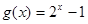 在区间
在区间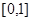 上是否为“友谊函数,只要检验函数
上是否为“友谊函数,只要检验函数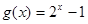 在
在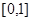 上是否满足(1)
上是否满足(1)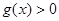 ;(2)
;(2)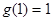 ;(3)
;(3)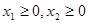 ,且
,且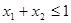 时,有
时,有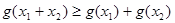 即可.
即可.(3)由
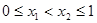 ,则
,则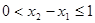 ,故有
,故有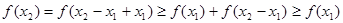 ,即得结论成立;
,即得结论成立;(1)令
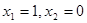 ,则
,则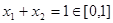 .由③,得
.由③,得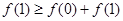 ,即
,即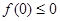 .又由①,得
.又由①,得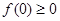 ,所以
,所以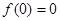 .
.(2)
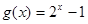 是友谊函数.任取
是友谊函数.任取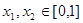 ,
,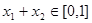 ,有
,有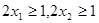 .则
.则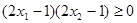 .即
.即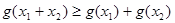 .又
.又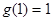 ,故
,故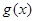 在
在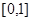 上为友谊函数.
上为友谊函数.(3)取
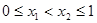 ,则
,则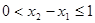 .因此,
.因此,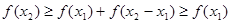 .假设
.假设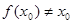 ,若
,若 ,则
,则 .若
.若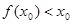 ,则
,则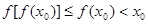 .都与题设矛盾,因此
.都与题设矛盾,因此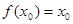 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
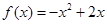 .
.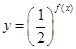 的最小值;
的最小值;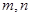 ,当
,当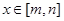 时,
时,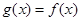 ,且
,且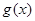 的值域为
的值域为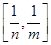 ?若存在,求出所有的
?若存在,求出所有的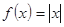 ,则下列哪个函数与
,则下列哪个函数与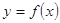 表示同一个函数( )
表示同一个函数( )


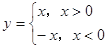
 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 ;
; 满足:
满足: ,则
,则 =__________.
=__________. ,
, ,
, 的最小值为
的最小值为 .
. ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;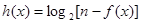 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[ ”的单调递增函数是( )
”的单调递增函数是( )



 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完. (万元)关于年产量
(万元)关于年产量 有且仅有一个解
有且仅有一个解