题目内容
设二次函数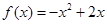 .
.
(1)求函数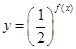 的最小值;
的最小值;
(2)问是否存在这样的正数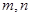 ,当
,当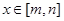 时,
时,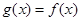 ,且
,且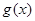 的值域为
的值域为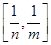 ?若存在,求出所有的
?若存在,求出所有的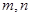 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
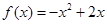 .
.(1)求函数
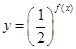 的最小值;
的最小值;(2)问是否存在这样的正数
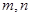 ,当
,当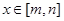 时,
时,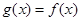 ,且
,且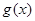 的值域为
的值域为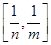 ?若存在,求出所有的
?若存在,求出所有的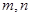 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)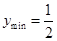 ;(2)
;(2)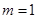 ,
,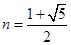 .
.
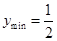 ;(2)
;(2)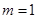 ,
,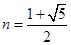 .
.试题分析:(1)这里遇到的是复合函数的最值问题,它是由简单的二次函数与指数函数复合而成的,遵循由内到外的解题顺序,很容易求出最小值;(2)这里是含参数的问题,常规方法是对参数分类讨论,如何分类,即分类的标准是什么?这是重点和难点,看解析往往是知其然,不知其所以然,这里的分类标准是将动区间
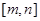 与二次函数
与二次函数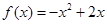 的定对称轴
的定对称轴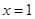 进行比较,自然就会分出它们有三种相对位置关系,即对称轴
进行比较,自然就会分出它们有三种相对位置关系,即对称轴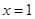 分别在区间
分别在区间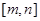 的左、中、右,故讨论分三种情形,当然讨论必须遵守不重不漏的原则,因此我们还必须关注细节,如区间的端点等,学会讨论重要,学会回避讨论更重要,它对化繁为简的能力要求非常高,这里的解法一是分类讨论的,而解法二就回避了讨论,解得很简洁,用心体会一下.
的左、中、右,故讨论分三种情形,当然讨论必须遵守不重不漏的原则,因此我们还必须关注细节,如区间的端点等,学会讨论重要,学会回避讨论更重要,它对化繁为简的能力要求非常高,这里的解法一是分类讨论的,而解法二就回避了讨论,解得很简洁,用心体会一下.试题解析:(1)
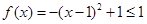 ,令
,令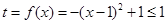
则
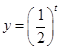 为
为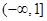 上减函数,因此,则当
上减函数,因此,则当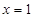 时,
时,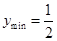 4分
4分(2)法一:
①当
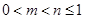 时,
时,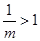
而当
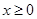 时,
时,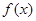 的最大值为
的最大值为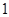 ,故此时不可能使
,故此时不可能使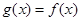 ,且
,且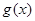 的值域为
的值域为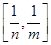 .7分
.7分②当
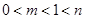 时,
时,则
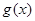 最大值为
最大值为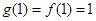 ,即
,即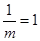 ,
,得
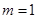 与
与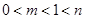 矛盾,故此时不可能. 10分
矛盾,故此时不可能. 10分③当
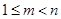 时,
时,∵
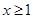 ,
,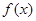 为减函数,则
为减函数,则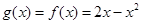
于是
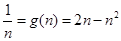 ,即
,即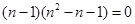 ,
,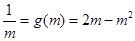
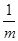 ,即
,即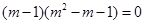
∵
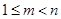 ,∴
,∴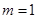 ,
,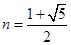 13分
13分综上所述,
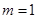 ,
,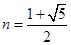 . 14分
. 14分法二:
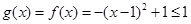 ,
,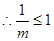 ,即
,即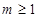 ,即
,即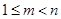 ,
,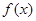 为
为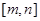 减函数,
减函数,于是
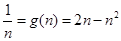 ,即
,即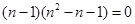 ,
,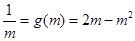
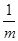 ,即
,即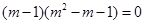
∵
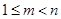 ,∴
,∴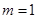 ,
,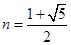 14分
14分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙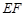 隔开,使得
隔开,使得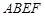 为矩形,
为矩形,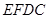 为正方形,设
为正方形,设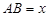 米,已知围墙(包括
米,已知围墙(包括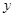 元。
元。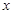 的函数解析式;
的函数解析式;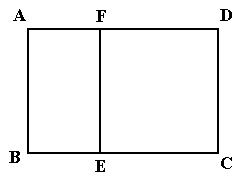
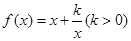 ,
,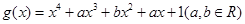 ,(1)若
,(1)若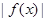 的最小值为2,求
的最小值为2,求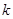 值;(2)设函数
值;(2)设函数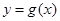 有零点,求
有零点,求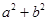 的最小值.
的最小值.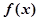 若存在
若存在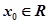 ,
,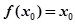 成立,则称
成立,则称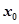 为
为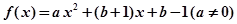
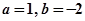 时,求函数
时,求函数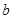 ,函数
,函数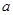 的取值范围.
的取值范围.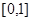 的函数
的函数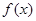 同时满足以下三个条件:
同时满足以下三个条件: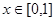 ,总有
,总有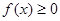 ;
;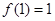 ;
; 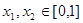 ,且
,且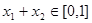 时,
时,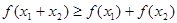 成立.
成立.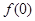 的值;
的值;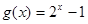 在区间
在区间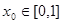 ,使得
,使得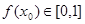 ,且
,且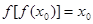 ,求证:
,求证: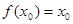 .
.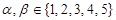 ,那么使得
,那么使得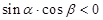 的数对
的数对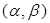 有 个.
有 个.