题目内容
已知二次函数 ,
, ,
, 的最小值为
的最小值为 .
.
⑴求函数 的解析式;
的解析式;
⑵设 ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
⑶设函数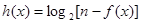 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[
 ,
, ,
, 的最小值为
的最小值为 .
.⑴求函数
 的解析式;
的解析式;⑵设
 ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;⑶设函数
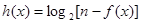 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[(1)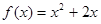 ;(2)
;(2)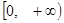 ;(3)
;(3)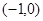 。
。
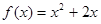 ;(2)
;(2)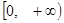 ;(3)
;(3)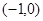 。
。 试题分析:(1)由
 可设
可设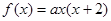 ,再由
,再由 的最小值
的最小值 求a的值;(2)首先对
求a的值;(2)首先对二次项系数分
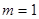 、
、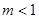 、
、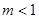 三种情况讨论,然后确定对称轴
三种情况讨论,然后确定对称轴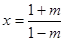 与给定区间
与给定区间 端点的关系;(3)要满足题意,须有
端点的关系;(3)要满足题意,须有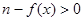 有解,且
有解,且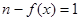 无解.然后求
无解.然后求 的最小值,令
的最小值,令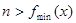 ,但
,但 不属于
不属于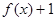 的值域,即可得实数
的值域,即可得实数 的取值范围。
的取值范围。⑴ 由题意设
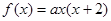 ,
,∵
 的最小值为
的最小值为 , ∴
, ∴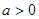 ,且
,且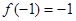 , ∴
, ∴ 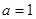 ,
,∴
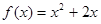 .
.⑵ ∵
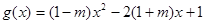 ,
,①当
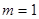 时,
时,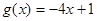 在[-1, 1]上是减函数,∴
在[-1, 1]上是减函数,∴ 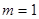 符合题意.
符合题意.② 当
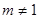 时,对称轴方程为:
时,对称轴方程为: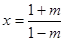 ,
,ⅰ)当
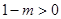 ,即
,即 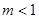 时,抛物线开口向上,
时,抛物线开口向上,由
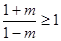 , 得
, 得 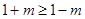 , ∴
, ∴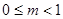 ;
;ⅱ)当
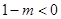 , 即
, 即 时,抛物线开口向下,
时,抛物线开口向下,由
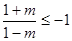 ,得
,得 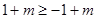 , ∴
, ∴ .
.综上知,实数
 的取值范围为
的取值范围为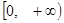 .
.⑶法一:∵ 函数
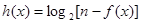 在定义域内不存在零点,必须且只须有
在定义域内不存在零点,必须且只须有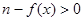 有解,且
有解,且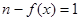 无解.
无解.∴
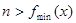 ,且
,且 不属于
不属于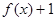 的值域,
的值域,又∵
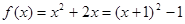 ,
,∴
 的最小值为
的最小值为 ,
,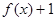 的值域为
的值域为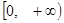 ,
,∴
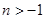 ,且
,且
∴
 的取值范围为
的取值范围为 .
.法二:
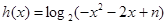 ,令
,令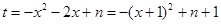 ,
,必有
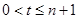 ,得
,得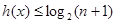 ,
,因为函数
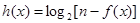 在定义域内不存在零点,
在定义域内不存在零点,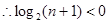 ,
,得
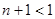 ,即
,即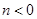 ,又
,又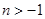 (否则函数定义域为空集,不是函数),
(否则函数定义域为空集,不是函数),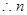 的取值范围是
的取值范围是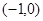 。
。
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙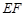 隔开,使得
隔开,使得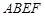 为矩形,
为矩形,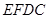 为正方形,设
为正方形,设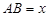 米,已知围墙(包括
米,已知围墙(包括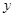 元。
元。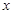 的函数解析式;
的函数解析式;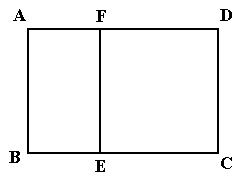
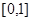 的函数
的函数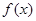 同时满足以下三个条件:
同时满足以下三个条件: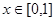 ,总有
,总有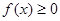 ;
;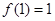 ;
; 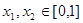 ,且
,且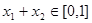 时,
时,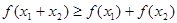 成立.
成立.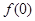 的值;
的值;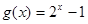 在区间
在区间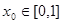 ,使得
,使得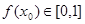 ,且
,且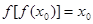 ,求证:
,求证: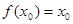 .
.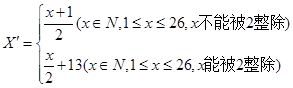
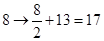 ,即
,即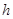 变成
变成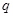 ;如
;如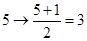 ,即
,即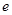 变成
变成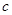 .
.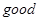 译成的密文是什么?
译成的密文是什么?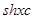 ,那么原来的明文是什么?
,那么原来的明文是什么? =m?
=m? +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.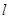 与曲线
与曲线 满足下列两个条件:
满足下列两个条件: 直线
直线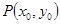 处与曲线
处与曲线 曲线
曲线 附近位于直线
附近位于直线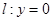 在点
在点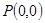 处“切过”曲线
处“切过”曲线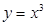
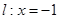 在点
在点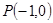 处“切过”曲线
处“切过”曲线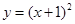
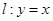 在点
在点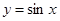
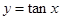
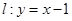 在点
在点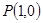 处“切过”曲线
处“切过”曲线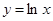
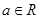 ,函数
,函数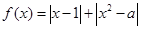 ,若
,若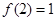 ,则
,则 .
.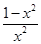 (x≠0),则f(
(x≠0),则f(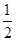 )等于( )
)等于( )