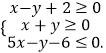题目内容
【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下: 5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
(Ⅰ)写出m,n的值,若该“微信运动”团队共有120人,请估计该团队中一天行走步数不少于7500步的人数;
(Ⅱ)记C组步数数据的平均数与方差分别为v1 , ![]() ,E组步数数据的平均数与方差分别为v2 ,
,E组步数数据的平均数与方差分别为v2 , ![]() ,试分别比较v1与v2 ,
,试分别比较v1与v2 , ![]() 与
与 ![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
【答案】解:(Ⅰ)利用对这20个数据按组距1000进行分组,得到m=4,n=2, 估计该团队中一天行走步数不少于7500步的人数为:120× ![]() =48人.
=48人.
(Ⅱ)v1<v2 , ![]() >
> ![]() .
.
(Ⅲ)A组两个数据为5860,6460,E组两个数据为9860,9860
任取两个数据,可能的组合为(5860,6460)、(5860,9860)、(5860,9860)、
(6460,9860)、(6460,9860)、(9860,9860),共6种结果
记步数差的绝对值大于3000为事件A
A={(5860,9860)、(5860,9860)、(6460,9860)、(6460,9860)}共包括4种结果
所以 ![]() .
.
【解析】(Ⅰ)利用对这20个数据按组距1000进行分组,得到m=4,n=2,利用等可能事件概率计算公式能估计该团队中一天行走步数不少于7500步的人数.(Ⅱ)由平均数与方差的性质能比较v1与v2 , ![]() 与
与 ![]() 的大小.(Ⅲ)A组两个数据为5860,6460,E组两个数据为9860,9860,任取两个数据,利用列举法能求出这2个数据步数差的绝对值大于3000步的概率.
的大小.(Ⅲ)A组两个数据为5860,6460,E组两个数据为9860,9860,任取两个数据,利用列举法能求出这2个数据步数差的绝对值大于3000步的概率.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案