题目内容
已知函数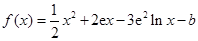 在
在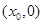 处的切线斜率为零.
处的切线斜率为零.
(Ⅰ)求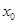 和
和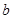 的值;
的值;
(Ⅱ)求证:在定义域内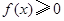 恒成立;
恒成立;
(Ⅲ) 若函数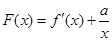 有最小值
有最小值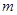 ,且
,且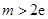 ,求实数
,求实数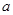 的取值范围.
的取值范围.
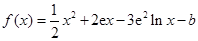 在
在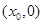 处的切线斜率为零.
处的切线斜率为零.(Ⅰ)求
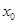 和
和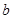 的值;
的值;(Ⅱ)求证:在定义域内
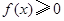 恒成立;
恒成立;(Ⅲ) 若函数
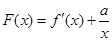 有最小值
有最小值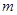 ,且
,且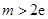 ,求实数
,求实数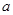 的取值范围.
的取值范围.(Ⅰ)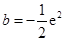 .(Ⅱ)证明:见解析;(Ⅲ)
.(Ⅱ)证明:见解析;(Ⅲ) 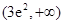 .
.
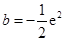 .(Ⅱ)证明:见解析;(Ⅲ)
.(Ⅱ)证明:见解析;(Ⅲ) 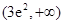 .
.(I)根据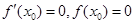 求出x0和b的值.
求出x0和b的值.
(II)利用导数研究出f(x)的最小值,证明f(x)的最小值不小于零即可.
(III)先求出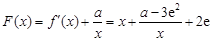
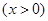 ,然后分
,然后分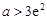 、
、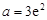 和
和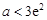 三种情况求其最小值m,根据m>2e,求出a的取值范围.
三种情况求其最小值m,根据m>2e,求出a的取值范围.
(Ⅰ)解: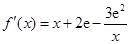 .
.
由题意有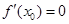 即
即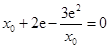 ,解得
,解得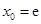 或
或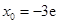 (舍去).
(舍去).
得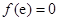 即
即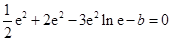 ,解得
,解得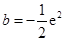 .
.
(Ⅱ)证明:由(Ⅰ)知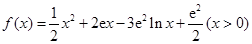 ,
,
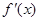
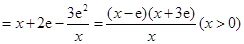 .在区间
.在区间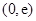 上,有
上,有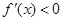 ;在区间
;在区间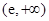 上,有
上,有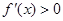 . 故
. 故 在
在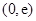 单调递减,在
单调递减,在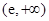 单调递增,
单调递增,
于是函数 在
在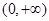 上的最小值是
上的最小值是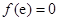 .
.
故当 时,有
时,有 恒成立.
恒成立.
(Ⅲ)解: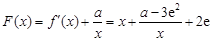
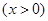 .
.
当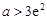 时,则
时,则 ,当且仅当
,当且仅当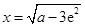 时等号成立,故
时等号成立,故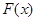 的最小值
的最小值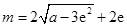
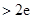 ,符合题意;
,符合题意;
当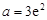 时,函数
时,函数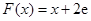 在区间
在区间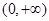 上是增函数,不存在最小值,不合题意;
上是增函数,不存在最小值,不合题意;
当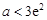 时,函数
时,函数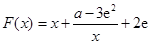 在区间
在区间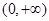 上是增函数,不存在最小值,不合题意.综上,实数
上是增函数,不存在最小值,不合题意.综上,实数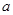 的取值范围
的取值范围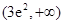 .
.
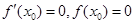 求出x0和b的值.
求出x0和b的值.(II)利用导数研究出f(x)的最小值,证明f(x)的最小值不小于零即可.
(III)先求出
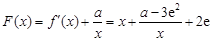
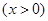 ,然后分
,然后分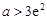 、
、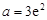 和
和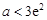 三种情况求其最小值m,根据m>2e,求出a的取值范围.
三种情况求其最小值m,根据m>2e,求出a的取值范围.(Ⅰ)解:
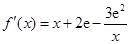 .
. 由题意有
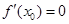 即
即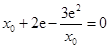 ,解得
,解得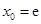 或
或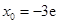 (舍去).
(舍去).得
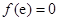 即
即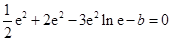 ,解得
,解得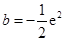 .
.(Ⅱ)证明:由(Ⅰ)知
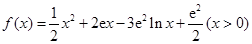 ,
,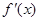
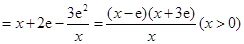 .在区间
.在区间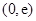 上,有
上,有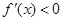 ;在区间
;在区间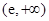 上,有
上,有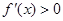 . 故
. 故 在
在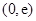 单调递减,在
单调递减,在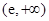 单调递增,
单调递增,于是函数
 在
在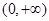 上的最小值是
上的最小值是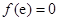 .
.故当
 时,有
时,有 恒成立.
恒成立.(Ⅲ)解:
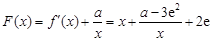
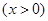 .
.当
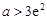 时,则
时,则 ,当且仅当
,当且仅当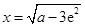 时等号成立,故
时等号成立,故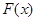 的最小值
的最小值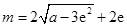
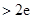 ,符合题意;
,符合题意;当
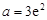 时,函数
时,函数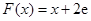 在区间
在区间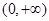 上是增函数,不存在最小值,不合题意;
上是增函数,不存在最小值,不合题意;当
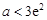 时,函数
时,函数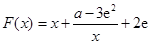 在区间
在区间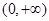 上是增函数,不存在最小值,不合题意.综上,实数
上是增函数,不存在最小值,不合题意.综上,实数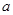 的取值范围
的取值范围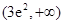 .
.
练习册系列答案
相关题目
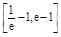 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;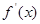 是函数
是函数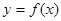 的导函数,且
的导函数,且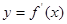 的图像如图所示,
的图像如图所示,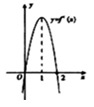
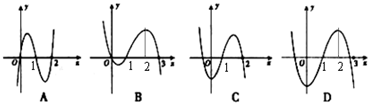

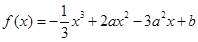 (常数a,b满足0<a<1,b
(常数a,b满足0<a<1,b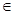 R)
R)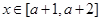 ,不等式|
,不等式| a恒成立,求a的取值范围。
a恒成立,求a的取值范围。 ,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( ) .
.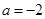 时,求函数
时,求函数 的单调区间;
的单调区间; ,使得函数
,使得函数 ?若存在,,求
?若存在,,求 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸 ,则称
,则称 时,利用定义分析
时,利用定义分析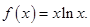
 的极值点;
的极值点;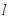 过点
过点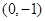 且与曲线
且与曲线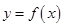 相切,求直线
相切,求直线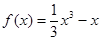 在
在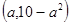 上有最小值,则实数
上有最小值,则实数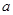 的取值范围是 .
的取值范围是 .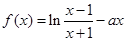 在
在 上单调递增,则实数a的取值范围是 .
上单调递增,则实数a的取值范围是 .