题目内容
9.已知过点$P({-2\sqrt{3},-2})$的直线l与圆O:x2+y2=4有公共点,则直线l斜率的取值范围是$[{0,\sqrt{3}}]$.分析 设直线的斜率是k,利用直线和圆的位置关系即可得到结论.
解答 解:设直线的斜率是k,则直线方程为y+2=k(x+2$\sqrt{3}$),即kx-y+2$\sqrt{3}$k-2=0,
当直线和圆相切时,满足圆心到直线的距离d=$\frac{|2\sqrt{3}k-2|}{\sqrt{{k}^{2}+1}}$=2,
解得k=0或$\sqrt{3}$,
则直线l的斜率的取值范围为$[{0,\sqrt{3}}]$.
故答案为:$[{0,\sqrt{3}}]$.
点评 本题主要考查直线斜率的求解,根据直线和圆的位置关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.函数f(x)=$\left\{\begin{array}{l}{{a}^{x},(x>1)}\\{(4-\frac{a}{2})x+5,(x≤1)}\end{array}\right.$满足对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0成立,则实数a的取值范围是( )
| A. | (4,+∞) | B. | [6,8) | C. | (6,8) | D. | (1,8) |
4.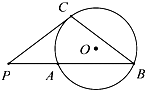 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )| A. | 3 | B. | 2 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
14.函数 y=cos2x+2cosx的值域是( )
| A. | [-1,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},-1]$ | D. | $[\frac{3}{2},3]$ |
18.在△ABC中,a=3,b=5,c=7,那么这个三角形的最大角是( )
| A. | 135° | B. | 150° | C. | 90° | D. | 120° |
19.圆x2+y2=1在伸缩变换$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$的作用下,所得方程是( )
| A. | 4x′2+9y′2=1 | B. | $\frac{{{{x'}^2}}}{2}+\frac{{{{y'}^2}}}{3}=1$ | C. | $\frac{{{{x'}^2}}}{9}+\frac{{{{y'}^2}}}{4}=1$ | D. | $\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$ |