Question

【题目】在某校科普知识竞赛前的模拟测试中，得到甲、乙两名学生的6次模拟测试成绩(百分制)的茎叶图.

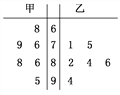
(I)若从甲、乙两名学生中选择一人参加该知识竞赛，你会选哪位？请运用统计学的知识说明理由；

(II)若从甲的6次模拟测试成绩中随机选择2个，记选出的成绩中超过87分的个数为随机变量ξ，求ξ的分布列和均值.

Answer 1

【答案】(Ⅰ)答案见解析；(Ⅱ)答案见解析.

【解析】试题分析：

(1)由题意考查两人的平均值均为82，方差甲乙分别为，结合方差可知乙的方差小，即乙发挥更稳定，故可选择学生乙参加知识竞赛.

(2)由题意可知：ξ的所有可能取值为0，1，2，结合超几何分布概率公式求得概率值，得到分布列，然后计算可得均值为.

试题解析：

(I)学生甲的平均成绩x甲＝＝82，

学生乙的平均成绩x乙＝＝82，

又s＝×[(68-82)2＋(76-82)2＋(79-82)2＋(86-82)2＋(88-82)2＋(95-82)2]＝77，

s＝×[(71-82)2＋(75-82)2＋(82-82)2＋(84-82)2＋(86-82)2＋(94-82)2]＝，

则x甲＝x乙，s>s，说明甲、乙的平均水平一样，但乙的方差小，即乙发挥更稳定，故可选择学生乙参加知识竞赛.

(II)随机变量ξ的所有可能取值为0，1，2，且

P(ξ＝0)＝＝，P(ξ＝1)＝＝，P (ξ＝2)＝＝，

则ξ的分布列为

ξ	0	1	2
P

所以均值E(ξ)＝0×＋1×＋2×＝.