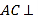题目内容
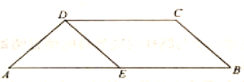
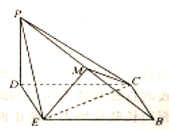
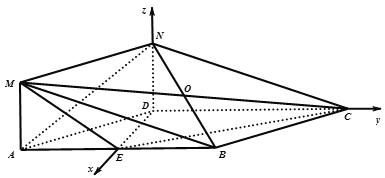
【题目】如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上的动点,二面角
上的动点,二面角![]() 的平面角的大小为30°,求线段
的平面角的大小为30°,求线段![]() 的长.
的长.
【答案】(Ⅰ)证明见解析:(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由已知可得四边形![]() 为平行四边形,连
为平行四边形,连![]() ,与
,与![]() 交于
交于![]() ,则点
,则点![]() 为
为![]() 的中点,连
的中点,连![]() ,结合已知可证
,结合已知可证![]() ,即可证明结论;
,即可证明结论;
(Ⅱ)由已知可得![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,确定
为坐标原点建立空间直角坐标系,确定![]() 的坐标,求出平面
的坐标,求出平面![]() 一个法向量坐标,按照空间向量线面角公式即可求解;
一个法向量坐标,按照空间向量线面角公式即可求解;
(Ⅲ)设![]() ,求出平面
,求出平面![]() 一个法向量的坐标,取平面
一个法向量的坐标,取平面![]() 的法向量为
的法向量为![]() ,按照空间向量的面面角公式,即可求出结论.
,按照空间向量的面面角公式,即可求出结论.
(Ⅰ)![]() 四边形
四边形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,连
为平行四边形,连![]() ,与
,与![]() 交于
交于![]() ,
,
则点![]() 为
为![]() 的中点,连
的中点,连![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;
(Ⅱ)![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() ,又
,又![]() 平面
平面![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,
建立空间直角坐标系![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则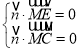 ,即
,即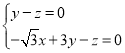 ,
,
令![]() ,则
,则![]() ,
,
![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)设![]() ,
,
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,即
,即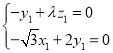 ,
,
令![]() ,则
,则![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以线段![]() 的长为
的长为![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】双十一购物狂欢节,是指每年11月11日的网络促销日,源于淘宝商城(天猫)2009年11月11日举办的网络促销活动,已成为中国电子商务行业的年度盛事.某生产商为了了解其生产的产品在不同电商平台的销售情况,统计了![]() 两个电商平台各十个网络销售店铺的销售数据:
两个电商平台各十个网络销售店铺的销售数据:
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
(1)作出![]() 两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
(2)填写下面关于店铺个数的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为销售量与电商平台有关;
的把握认为销售量与电商平台有关;
销售量 | 销售量 | 总计 | |
| |||
| |||
总计 |
(3)生产商要从这20个网络销售店铺销售量前五名的店铺中,随机抽取三个店铺进行销售返利,则其中恰好有两个店铺的销售量在95以上的概率是多少?
附: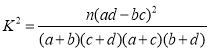 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |