题目内容
【题目】已知圆C1的圆心在坐标原点O，且恰好与直线
相切．
(Ⅰ)求圆C1的标准方程；
(Ⅱ)设点A为圆上一动点，AN垂直于x轴于点N，若动点Q满足
(其中m为非零常数)，试求动点Q的轨迹方程；
(Ⅲ)在(Ⅱ)的结论下，当m＝
时，得到动点Q的轨迹为曲线C，与l1垂直的直线l与曲线C交于B，D两点，求△OBD面积的最大值．
【答案】(Ⅰ) 圆C1的方程为x2＋y2＝4;(Ⅱ) 点Q的轨迹方程为
;(Ⅲ)
.
【解析】分析：（Ⅰ）由题意首先求得圆的半径为r＝2，结合圆心坐标可得圆C1的方程为x2＋y2＝4.
（Ⅱ）设动点Q(x，y)，A(x0，y0)，由题意可得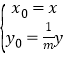
，则动点Q的轨迹方程为.
（Ⅲ）由题意结合(Ⅱ)的结论可知曲线C的方程为
,联立直线方程与椭圆方程可得7x2－8bx＋4b2－12＝0.结合韦达定理和弦长公式可得面积函数为：
，则△OBD面积的最大值为 .
详解：（Ⅰ）设圆的半径为r，圆心到直线l1的距离为d，
则d＝
＝2.
因为r＝d＝2，圆心为坐标原点O，
所以圆C1的方程为x2＋y2＝4.
（Ⅱ）设动点Q(x，y)，A(x0，y0)，
∵AN⊥x轴于点N，∴N(x0,0)，
由题意知，(x，y)＝m(x0，y0)＋(1－m)·(x0,0)，
解得
即
将点A
代入圆C1的方程x2＋y2＝4，
得动点Q的轨迹方程为
＋
＝1.
（Ⅲ）当m＝
时，曲线C的方程为＋
＝1，
设直线l的方程为y＝－x＋b，直线l与椭圆＋＝1交点B(x1，y1)，D(x2，y2)，
联立方程
得7x2－8bx＋4b2－12＝0.
因为Δ＝48(7－b2)>0，
解得b2<7，且x1＋x2＝
，x1x2＝
.
又因为点O到直线l的距离d1＝
，
|BD|＝
·
＝
.
所以S△OBD＝
··
＝
≤
，
当且仅当b2＝7－b2，
即b2＝
<7时取到最大值．
所以△OBD面积的最大值为 .
