题目内容
【题目】已知函数f（x）=|x+a|+|x+ 
|（a＞0）（a＜0）
（1）当a=2时，求不等式f（x）＞3的解集
（2）证明： 
．
【答案】
（1）解：当a=2时，f（x）=|x+2|+|x+ 
|，原不等式等价于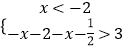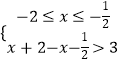 
或 
或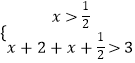 
解得：x＜﹣ 
或x∈或 
，所以不等式的解集为{x|x＜﹣ 或 
（2）解：f（m）+f（﹣ 
）=|m+a|+|m+ 
|+|﹣ +a|+|﹣ + |
= 
【解析】（1）分类讨论，解不等式，即可得出结论；（2）f（m）+f（﹣ ）=|m+a|+|m+ |+|﹣ +a|+|﹣ + |，利用三角不等式，及基本不等式即可证明结论．
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识，掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号，以及对不等式的证明的理解，了解不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
【题目】通过随机调查询问110名性别不同的高中生是否爱好某项运动，得到如下的列联表：
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 
计算得 
附表：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是( )
A.在犯错误的概率不超过0.1％的前提下，认为“爱好该项运动与性别无关”
B.在犯错误的概率不超过0.1％的前提下，认为“爱好该项运动与性别有关”
C.有99％以上的把握认为“爱好该项运动与性别无关”
D.有99％以上的把握认为“爱好该项运动与性别有关”
