Question

【题目】抛物线x2=ay（a＞0）的准线l与y轴交于点P，若l绕点P以每秒 弧度的角速度按逆时针方向旋转t秒钟后，恰与抛物线第一次相切，则t等于（ ）
A.1
B.2
C.3
D.4

Answer 1

【答案】C
【解析】解：根据抛物线的方程x2=ay，得到p= ，
所以此抛物线的准线方程为y=﹣ ，P坐标为（0，﹣ ），
令恒过P点的直线y=kx﹣ 与抛物线相切，
联立直线与抛物线得 ，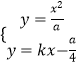
消去y得： ﹣kx+ =0，得到△=k2﹣1=0，即k2=1，
解得：k=1或k=﹣1，
由直线l绕点P逆时针旋转，k=﹣1不合题意，舍去，
则k=1，此时直线的倾斜角为 ，又P的角速度为每秒 弧度，
所以直线l恰与抛物线第一次相切，则t= =3．
故选C．