题目内容
7.化简:(1)sin($\frac{π}{2}$+α)cos2($\frac{π}{2}$+α)sin(3π-α)tan(π+α);
(2)$\frac{sin(-4π+α)cos(π-α)cos(\frac{π}{2}+α)sin(\frac{11π}{2}-α)}{sin(-\frac{π}{2}-α)cos(3π-α)cos(\frac{9π}{2}+α)sin(π+α)}$.
分析 (1)原式各项利用诱导公式化简,计算即可得到结果;
(2)原式分子分母利用诱导公式化简,约分即可得到结果.
解答 解:(1)原式=cosα•sin2α•sinα•tanα=cosα•sin2α•sinα•$\frac{sinα}{cosα}$=sin4α;
(2)原式=$\frac{sinα(-cosα)(-sinα)(-cosα)}{-cosα(-cosα)(-sinα)(-sinα)}$=-1.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.复数$z=3i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
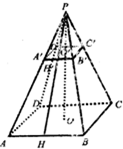 如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.
如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.