题目内容
9．解关于x的不等式x2-（2+a）x+2a＜0．分析 把不等式化为（x-2）（x-a）＜0，讨论a的取值范围，求出不等式的解集即可．
解答 解：不等式x2-（2+a）x+2a＜0可化为
（x-2）（x-a）＜0，
所以，当a=2时，不等式为（x-2）2＜0，解集为∅；
当a＞2时，不等式的解集为{x|2＜x＜a}，
当a＜2时，不等式的解集为{x|a＜x＜2}．
点评 本题考查了利用分类讨论思想解含有字母系数的不等式的解法与应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
20．若sinα=$\frac{3}{5}$，且α是第二象限角，则tanα=（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $±\frac{4}{3}$ | D． | $±\frac{3}{4}$ |
17．方程x2-4y2+3x-6y=0表示的图形是（ ）
| A． | 一条直线 | B． | 两条直线 | C． | 一个圆 | D． | 以上答案都不对 |
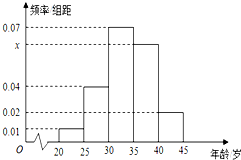为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25），[25，30），[30，35），[35，40），[40，45]．