��Ŀ����
19��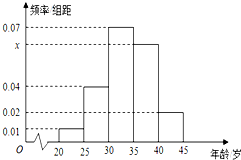 Ϊ��ǿ����Ľ��ܻ�����ʶ��ij������ȫ��������������־Ը�ߣ��ӷ���������500��־Ը���������ȡ100��־Ը�ߣ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������������ǣ�[20��25����[25��30����[30��35����[35��40����[40��45]��
Ϊ��ǿ����Ľ��ܻ�����ʶ��ij������ȫ��������������־Ը�ߣ��ӷ���������500��־Ը���������ȡ100��־Ը�ߣ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������������ǣ�[20��25����[25��30����[30��35����[35��40����[40��45]��������ͼ��x��ֵ������Ƶ�ʷֲ�ֱ��ͼ������500��־Ը����������[35��40�����������
�����ڳ����100��־Ը���а�������÷ֲ�����ķ�����ȡ20���μ����Ĺ㳡����������ٴ���20���в��ü������������ѡȡ3��־Ը�ߵ�����Ҫ�����ˣ�����3��־Ը���С��������35�ꡱ������ΪX����X�ķֲ��м���ѧ������
���� ��I������С���ε��������Ƶ�ʼ��㼴�ý��ۣ�
��II�����÷ֲ�����ķ�������ѡȡ20������֪X�Ŀ���ȡֵΪ0��1��2��3����������ɵý��ۣ�
��� �⣺��I����С���ε��������Ƶ�ʣ�
���[35��40�����Ƶ�ʺ�Ϊ0.70��
��$x=\frac{1-0.70}{5}=0.06$��
��500��־Ը����������[35��40���������Ϊ0.06��5��500=150���ˣ���
��II���÷ֲ�����ķ���������ѡȡ20����
���������䡰����35�ꡱ������12����
�����䲻����35�ꡱ������8����
��X�Ŀ���ȡֵΪ0��1��2��3��
��$P��{X=0}��=\frac{C_8^3}{{C_{20}^3}}=\frac{14}{285}$��
$P��{X=1}��=\frac{{C_{12}^1C_8^2}}{{C_{20}^3}}=\frac{28}{95}$��
$P��{X=2}��=\frac{{C_{12}^2C_8^1}}{{C_{20}^3}}=\frac{44}{95}$��
$P��{X=3}��=\frac{{C_{12}^3}}{{C_{20}^3}}=\frac{11}{57}$��
��X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 |
| P | $\frac{14}{285}$ | $\frac{28}{95}$ | $\frac{44}{95}$ | $\frac{11}{57}$ |
���� ���⿼����ɢ�����������������ע����ⷽ���Ļ��ۣ������е��⣮

��ϰ��ϵ�д�
�����Ŀ
10�����ĸ���Ϸ�̣�������ˮƽ���Ⱥ���������һ��С��������С��������Ӱ���֣�����н���Ҫ���н��������Ӧѡ�����Ϸ���ǣ�������
| A�� |  | B�� |  | C�� |  | D�� |  |
14��f��x��=sinx+tanx+2��x��[-$\frac{��}{4}$��$\frac{��}{4}$]��f��x�����ֵΪM����СֵΪm��M+mΪ��������
| A�� | 4 | B�� | -4 | C�� | 2 | D�� | 0 |
11����֪����{an}���㣺${a_1}=\frac{1}{7}$�����������n��N*��${a_{n+1}}=\frac{7}{2}{a_n}��1-{a_n}��$����a999-a888=��������
| A�� | $-\frac{2}{7}$ | B�� | $\frac{2}{7}$ | C�� | $-\frac{3}{7}$ | D�� | $\frac{3}{7}$ |
8�����Ǧ�ʼ��Ϊx��Ǹ����ᣬ�ձ���һ��A��1��-$\sqrt{3}$������sin�����ڣ�������
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
9��ij���˶��������о��У�Ϊ�˸�ýӴ���������ί����ļ��18����־Ը�ߺ�12��Ů־Ը�ߣ����鷢�֣��С�Ů־Ը���зֱ���11�˺�5��ϲ���˶������ϲ����
��1���������������������2��2��������
��2�������������Ķ����Լ��飬�ܷ��ڷ�����ĸ��ʲ�����0.10��ǰ������Ϊ�Ա���ϲ���˶��йأ�
��3����Ů־Ը���г�ȡ2�˲μӽӴ�������������ϲ���˶�������Ϊ�Σ���εķֲ��к���ѧ����E�Σ�
�ο���ʽ��x2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$������n=a+b+c+d
�ο����ݣ�
��1���������������������2��2��������
| ϲ���˶� | ��ϲ���˶� | �ܼ� | |
| �� | 10 | 18 | |
| Ů | 5 | 12 | |
| �ܼ� | 30 |
��3����Ů־Ը���г�ȡ2�˲μӽӴ�������������ϲ���˶�������Ϊ�Σ���εķֲ��к���ѧ����E�Σ�
�ο���ʽ��x2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$������n=a+b+c+d
�ο����ݣ�
| P��x2��x0�� | 0.40 | 0.25 | 0.10 | 0.010 |
| x0 | 0.708 | 1.323 | 2.706 | 6.635 |