题目内容
【题目】做一个无盖的圆柱形水桶，若要使其体积是
，且用料最省，则圆柱的底面半径为__________．
【答案】
【解析】试题分析：设圆柱的高为h，半径为r则由圆柱的体积公式可得，πr2h=27π，即
，要使用料最省即求全面积的最小值，而S全面积=πr2+2πrh=
=
（法一）令S=f（r），结合导数可判断函数f（r）的单调性，进而可求函数取得最小值时的半径
（法二）：S全面积=πr2+2πrh==，利用基本不等式可求用料最小时的r
解：设圆柱的高为h，半径为r
则由圆柱的体积公式可得，πr2h=27π
S全面积=πr2+2πrh==
（法一）令S=f（r），（r＞0）
=
令f′（r）≥0可得r≥3，令f′（r）＜0可得0＜r＜3
∴f（r）在（0，3）单调递减，在[3，+∞）单调递增，则f（r）在r=3时取得最小值
（法二）：S全面积=πr2+2πrh=
=
=
=27π
当且仅当
即r=3时取等号
当半径为3时，S最小即用料最省
故答案为：3
阅读快车系列答案
【题目】某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
，
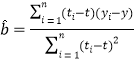【题目】心理学家分析发现“喜欢空间想象”与“性别”有关，某数学兴趣小组为了验证此结论，从全体组员中按分层抽样的方法抽取50名同学（男生30人、女生20人），给每位同学立体几何题、代数题各一道，让各位同学自由选择一道题进行解答，选题情况统计如下表：（单位：人）
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
（1）能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关？
（2）经统计得，选择做立体几何题的学生正答率为
，且答对的学生中男生人数是女生人数的5倍，现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究，求恰好抽到男女生各一人的概率．
附表及公式：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
