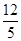题目内容
已知椭圆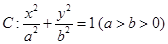 经过点
经过点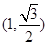 ,离心率为
,离心率为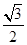 .
.
(1)求椭圆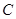 的方程;
的方程;
(2)直线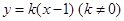 与椭圆
与椭圆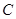 交于
交于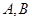 两点,点
两点,点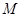 是椭圆
是椭圆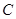 的右顶点.直线
的右顶点.直线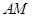 与直线
与直线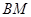 分别与
分别与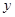 轴交于点
轴交于点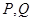 ,试问以线段
,试问以线段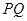 为直径的圆是否过
为直径的圆是否过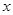 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
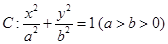 经过点
经过点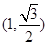 ,离心率为
,离心率为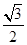 .
.(1)求椭圆
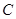 的方程;
的方程;(2)直线
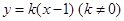 与椭圆
与椭圆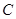 交于
交于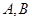 两点,点
两点,点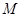 是椭圆
是椭圆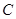 的右顶点.直线
的右顶点.直线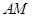 与直线
与直线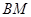 分别与
分别与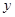 轴交于点
轴交于点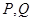 ,试问以线段
,试问以线段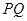 为直径的圆是否过
为直径的圆是否过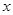 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.(1)椭圆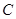 的方程是
的方程是 ;(2)线段
;(2)线段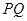 为直径的圆过
为直径的圆过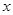 轴上的定点
轴上的定点 .
.
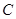 的方程是
的方程是 ;(2)线段
;(2)线段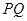 为直径的圆过
为直径的圆过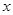 轴上的定点
轴上的定点 .
.试题分析:(1)求椭圆
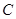 的方程,已知椭圆
的方程,已知椭圆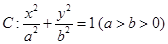 经过点
经过点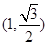 ,离心率为
,离心率为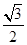 ,故可用待定系数法,利用离心率可得
,故可用待定系数法,利用离心率可得 ,利用过点
,利用过点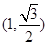 ,可得
,可得 ,再由
,再由 ,即可解出
,即可解出 ,从而得椭圆
,从而得椭圆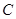 的方程;(2)这是探索性命题,可假设以线段
的方程;(2)这是探索性命题,可假设以线段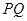 为直径的圆过
为直径的圆过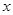 轴上的定点
轴上的定点 ,则
,则 ,故需表示出
,故需表示出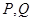 的坐标,因为点
的坐标,因为点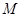 是椭圆
是椭圆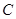 的右顶点,所以点
的右顶点,所以点 ,设
,设 ,分别写出直线
,分别写出直线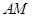 与的
与的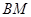 方程,得
方程,得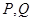 的坐标,由
的坐标,由 ,得
,得 ,因此由
,因此由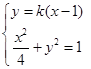 得
得 ,则
,则 式方程的根,利用根与系数关系得,
式方程的根,利用根与系数关系得, ,
, ,代入
,代入 即可.
即可.试题解析:(1)由题意得
 ,解得
,解得 ,
, .
.所以椭圆
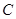 的方程是
的方程是 . 4分
. 4分(2)以线段
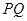 为直径的圆过
为直径的圆过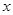 轴上的定点.
轴上的定点.由
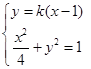 得
得 .
.设
 ,则有
,则有 ,
, .
.又因为点
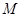 是椭圆
是椭圆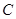 的右顶点,所以点
的右顶点,所以点 .
.由题意可知直线
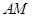 的方程为
的方程为 ,故点
,故点 .
.直线
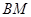 的方程为
的方程为 ,故点
,故点 .
.若以线段
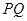 为直径的圆过
为直径的圆过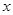 轴上的定点
轴上的定点 ,则等价于
,则等价于 恒成立.
恒成立. 又因为
 ,
, ,
,所以
 恒成立.
恒成立.又因为


 ,
,

 ,
,所以
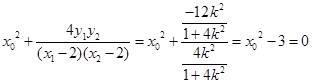 .解得
.解得 .
.故以线段
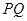 为直径的圆过
为直径的圆过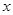 轴上的定点
轴上的定点 . 14分
. 14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :
: 的准线与
的准线与 轴交于点
轴交于点 ,焦点为
,焦点为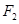 ;椭圆
;椭圆 以
以 .设
.设 是
是
 过
过 两点,且
两点,且 等于
等于 的周长,求
的周长,求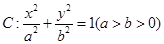 的短半轴长为
的短半轴长为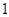 ,动点
,动点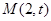
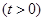 在直线
在直线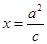 (
(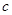 为半焦距)上.
为半焦距)上.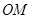 为直径且被直线
为直径且被直线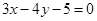 截得的弦长为
截得的弦长为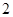 的圆的方程;
的圆的方程;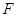 是椭圆的右焦点,过点
是椭圆的右焦点,过点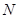 ,
,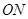 的长为定值,并求出这个定值.
的长为定值,并求出这个定值. :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 的直线
的直线 与椭圆
与椭圆 (点
(点 为椭圆
为椭圆 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.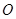 和点
和点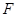 分别为椭圆
分别为椭圆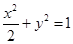 的中心和右焦点,点
的中心和右焦点,点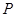 为椭圆上的任意一点,则
为椭圆上的任意一点,则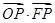 的最小值为( )
的最小值为( )


 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
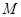 是椭圆
是椭圆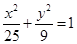 上的点,
上的点,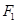 、
、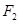 是椭圆的两个焦点,
是椭圆的两个焦点,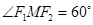 ,则
,则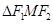 的面积等于______________.
的面积等于______________. ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______________.
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______________.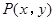 在椭圆
在椭圆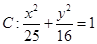 上,
上,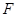 为椭圆
为椭圆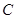 的右焦点,若点
的右焦点,若点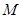 满足
满足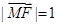 且
且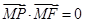 ,则
,则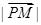 的最小值为( )
的最小值为( )