题目内容
已知椭圆 的短半轴长为
的短半轴长为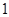 ,动点
,动点
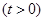 在直线
在直线 (
( 为半焦距)上.
为半焦距)上.
(1)求椭圆的标准方程;
(2)求以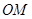 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为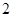 的圆的方程;
的圆的方程;
(3)设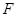 是椭圆的右焦点,过点
是椭圆的右焦点,过点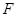 作
作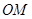 的垂线与以
的垂线与以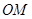 为直径的圆交于点
为直径的圆交于点 ,
,
求证:线段 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
 的短半轴长为
的短半轴长为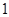 ,动点
,动点
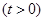 在直线
在直线 (
( 为半焦距)上.
为半焦距)上.(1)求椭圆的标准方程;
(2)求以
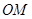 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为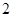 的圆的方程;
的圆的方程;(3)设
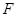 是椭圆的右焦点,过点
是椭圆的右焦点,过点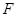 作
作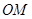 的垂线与以
的垂线与以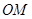 为直径的圆交于点
为直径的圆交于点 ,
,求证:线段
 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.(1)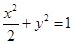 ,(2)
,(2) ,(3)
,(3)  .
.
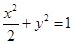 ,(2)
,(2) ,(3)
,(3)  .
.试题分析:(1)求椭圆标准方程,基本方法为待定系数法.由题意得
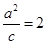 及
及 ,因此可解得
,因此可解得 ,
, .(2)圆的弦长问题,通常化为直角三角形,即半径、半弦长、圆心到直线距离构成一个直角三角形. 圆心为
.(2)圆的弦长问题,通常化为直角三角形,即半径、半弦长、圆心到直线距离构成一个直角三角形. 圆心为 ,圆心到直线
,圆心到直线 的距离
的距离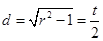 ,因此
,因此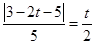 ,
, ,所求圆的方程为
,所求圆的方程为 . (3)涉及定值问题,一般通过计算,以算代证.本题有两种算法,一是利用射影定理,只需求出点
. (3)涉及定值问题,一般通过计算,以算代证.本题有两种算法,一是利用射影定理,只需求出点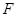 在
在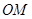 上射影
上射影 的坐标,即由两直线方程
的坐标,即由两直线方程 得
得 ,因此
,因此 .二是利用向量坐标表示,即设
.二是利用向量坐标表示,即设 ,根据两个垂直,消去参数t,确定
,根据两个垂直,消去参数t,确定 .
.试题解析:(1)由点
 在直线
在直线 上,得
上,得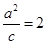 ,
,故
 , ∴
, ∴ . 从而
. 从而 . 2分
. 2分所以椭圆方程为
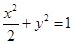 . 4分
. 4分(2)以
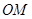 为直径的圆的方程为
为直径的圆的方程为 .
.即
 . 其圆心为
. 其圆心为 ,半径
,半径 . 6分
. 6分因为以
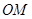 为直径的圆被直线
为直径的圆被直线 截得的弦长为
截得的弦长为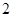 ,
,所以圆心到直线
 的距离
的距离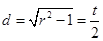 .
.所以
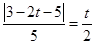 ,解得
,解得 .所求圆的方程为
.所求圆的方程为 . 9分
. 9分(3)方法一:由平几知:
 ,
,直线

 ,直线
,直线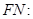
 ,
,由
 得
得 .
.∴
 .
.所以线段
 的长为定值
的长为定值 . 13分
. 13分方法二:设
 ,
,则
 .
. .
.又
 .
.所以,
 为定值. 13分
为定值. 13分
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 为椭圆
为椭圆
 右焦点,圆
右焦点,圆
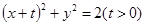 与椭圆
与椭圆 ,且直线
,且直线 与圆
与圆 相切于点
相切于点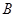 .
.
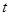 的值及椭圆
的值及椭圆 满足
满足 ,其中M、N是椭圆
,其中M、N是椭圆 为原点,直线OM与ON的斜率之积为
为原点,直线OM与ON的斜率之积为 ,求证:
,求证: 为定值.
为定值. 经过点
经过点 ,离心率为
,离心率为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,点
两点,点 是椭圆
是椭圆 与直线
与直线 分别与
分别与 轴交于点
轴交于点 ,试问以线段
,试问以线段 为直径的圆是否过
为直径的圆是否过 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.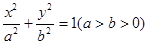 的左、右焦点,A、B是以O(O
的左、右焦点,A、B是以O(O B.
B.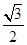 C.
C.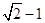 D.
D.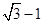
 的焦点为
的焦点为 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么 是
是 的( )
的( ) 倍
倍 倍
倍 倍
倍 倍
倍 的长轴的端点、焦点,则双曲线C的方程为_______.
的长轴的端点、焦点,则双曲线C的方程为_______. ,直线
,直线 与椭圆
与椭圆 恒有公共点,则实数
恒有公共点,则实数 的取值范围是
的取值范围是 =1的位置关系是________.
=1的位置关系是________. 是椭圆
是椭圆 上一点,
上一点, 为椭圆的一个焦点,且
为椭圆的一个焦点,且 轴,
轴, 焦距,则椭圆的离心率是
焦距,则椭圆的离心率是