题目内容
已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,

过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
(1)求椭圆方程;
(2)若圆N与x轴相切,求圆N的方程;
(3)设点R为圆N上的动点,点R到直线PF的最大距离为d,求d的取值范围.
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
(1)求椭圆方程;
(2)若圆N与x轴相切,求圆N的方程;
(3)设点R为圆N上的动点,点R到直线PF的最大距离为d,求d的取值范围.
(1)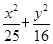 =1(2)
=1(2)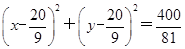 (3)
(3)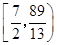
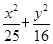 =1(2)
=1(2)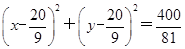 (3)
(3)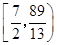
(1)∵e= 不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为
不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为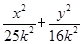 =1(a>b>0),∵P
=1(a>b>0),∵P 在椭圆上,∴
在椭圆上,∴ =1解得k=1,∴椭圆方程为
=1解得k=1,∴椭圆方程为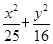 =1.
=1.
(2)kAP=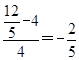 ,则直线AP的方程为y=-
,则直线AP的方程为y=-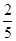 x+4,
x+4,
令y=t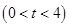 ,则x=
,则x=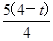 ∴M
∴M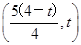 .∵Q(0,t)∴N
.∵Q(0,t)∴N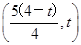 ,
,
∵圆N与x轴相切,∴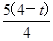 =t,由题意M为第一象限的点,则
=t,由题意M为第一象限的点,则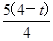 =t,解得t=
=t,解得t=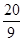 .∴N
.∴N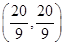 ,圆N的方程为
,圆N的方程为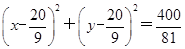 .
.
(3)F(3,0),kPF=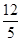 ,∴直线PF的方程为y=
,∴直线PF的方程为y=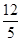 (x-3)即12x-5y-36=0,
(x-3)即12x-5y-36=0,
∴点N到直线PF的距离为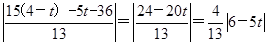 ,
,
∴d=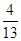
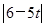 +
+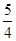 (4-t),∵0<t<4,
(4-t),∵0<t<4,
∴当0<t≤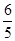 时,d=
时,d=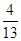 (6-5t)+
(6-5t)+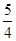 (4-t)=
(4-t)=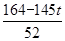 ,此时
,此时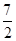 ≤d<
≤d<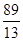 ,
,
当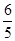 <t<4时,d=
<t<4时,d=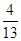 (5t-6)+
(5t-6)+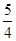 (4-t)=
(4-t)=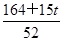 ,此时
,此时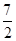 <d<
<d<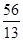 ,
,
∴综上,d的取值范围为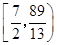 .
.
 不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为
不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为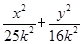 =1(a>b>0),∵P
=1(a>b>0),∵P 在椭圆上,∴
在椭圆上,∴ =1解得k=1,∴椭圆方程为
=1解得k=1,∴椭圆方程为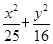 =1.
=1.(2)kAP=
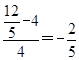 ,则直线AP的方程为y=-
,则直线AP的方程为y=-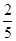 x+4,
x+4,令y=t
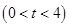 ,则x=
,则x=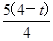 ∴M
∴M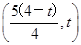 .∵Q(0,t)∴N
.∵Q(0,t)∴N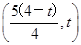 ,
,∵圆N与x轴相切,∴
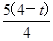 =t,由题意M为第一象限的点,则
=t,由题意M为第一象限的点,则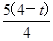 =t,解得t=
=t,解得t=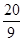 .∴N
.∴N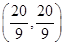 ,圆N的方程为
,圆N的方程为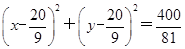 .
.(3)F(3,0),kPF=
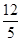 ,∴直线PF的方程为y=
,∴直线PF的方程为y=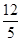 (x-3)即12x-5y-36=0,
(x-3)即12x-5y-36=0,∴点N到直线PF的距离为
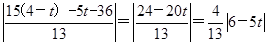 ,
,∴d=
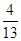
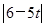 +
+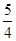 (4-t),∵0<t<4,
(4-t),∵0<t<4,∴当0<t≤
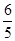 时,d=
时,d=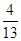 (6-5t)+
(6-5t)+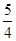 (4-t)=
(4-t)=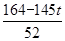 ,此时
,此时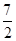 ≤d<
≤d<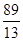 ,
,当
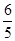 <t<4时,d=
<t<4时,d=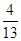 (5t-6)+
(5t-6)+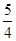 (4-t)=
(4-t)=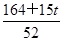 ,此时
,此时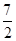 <d<
<d<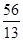 ,
,∴综上,d的取值范围为
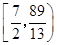 .
.
练习册系列答案
相关题目
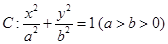 经过点
经过点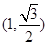 ,离心率为
,离心率为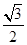 .
.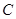 的方程;
的方程;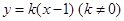 与椭圆
与椭圆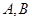 两点,点
两点,点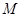 是椭圆
是椭圆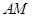 与直线
与直线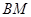 分别与
分别与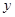 轴交于点
轴交于点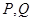 ,试问以线段
,试问以线段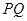 为直径的圆是否过
为直径的圆是否过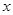 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.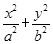 =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2=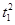 ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.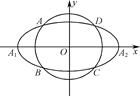
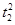 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: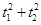 为定值.
为定值. ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆
相切,记动圆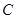 .
. ,过定点
,过定点 的动直线
的动直线 交轨迹
交轨迹 、
、 两点,
两点, 的外心为
的外心为 ,直线
,直线 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值.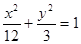 的焦点为
的焦点为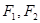 ,点
,点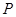 在椭圆上,如果线段
在椭圆上,如果线段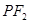 的中点在
的中点在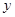 轴上,那么
轴上,那么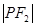 是
是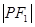 的( )
的( ) 倍
倍 倍
倍 倍
倍 倍
倍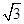 ,0)与定直线l1∶x=
,0)与定直线l1∶x=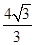 的距离之比为常数
的距离之比为常数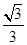 .
.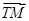 ·
· 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程.
 =1的位置关系是________.
=1的位置关系是________.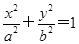 =1(a>b>0),点P
=1(a>b>0),点P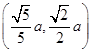 在椭圆上.
在椭圆上.