题目内容
(本题满分12分)
已知数列 满足
满足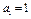 ,
,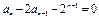 ,(
,(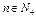 ,
,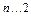 ).
).
(1)求证:数列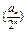 是等差数列;
是等差数列;
(2)若数列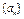 的前
的前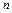 项和为
项和为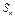 ,且
,且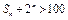 恒成立,求
恒成立,求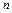 的最小值.
的最小值.
已知数列
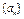 满足
满足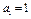 ,
,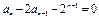 ,(
,(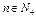 ,
,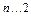 ).
).(1)求证:数列
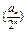 是等差数列;
是等差数列;(2)若数列
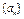 的前
的前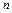 项和为
项和为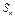 ,且
,且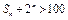 恒成立,求
恒成立,求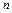 的最小值.
的最小值.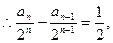
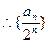 是以
是以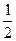 为首项,
为首项,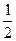 为公差的等差数列。 (4分)
为公差的等差数列。 (4分)(2)由(1):
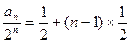
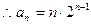 (6分)
(6分)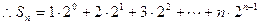 ①
①则
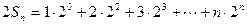 ②
②①—②,得
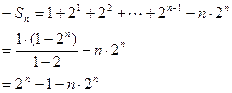
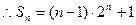 (9分)
(9分)由
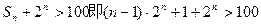 恒成立。
恒成立。得
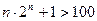 恒成立,
恒成立,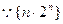 是单增数列,
是单增数列,且
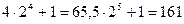
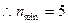 (12分)
(12分)略

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
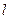 过点P
过点P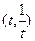 (
(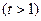 斜率为
斜率为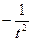 ,与直线
,与直线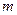 :
: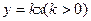 交于点A,与
交于点A,与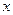 轴交于点B,点A,B的横坐标分别为
轴交于点B,点A,B的横坐标分别为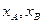 ,记
,记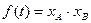 .
.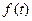 的解析式;
的解析式;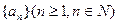 满足
满足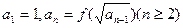 ,求数列
,求数列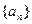 的通项公式;
的通项公式;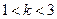 时,证明不等式
时,证明不等式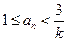 .
.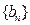 中,
中,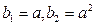
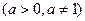 ,对于函数
,对于函数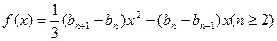 有
有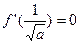
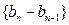 为等比数列,并求
为等比数列,并求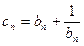 ,求和
,求和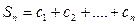
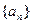 的前n项和为
的前n项和为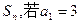 ,点
,点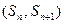 在直线
在直线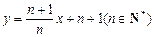
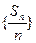 是等差数列;
是等差数列;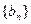 满足
满足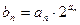 ,求数列
,求数列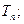
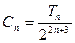 ,求证:
,求证: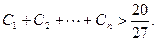
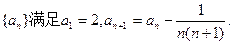
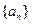 的通项公式;
的通项公式;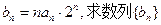 的前n项和Sn。
的前n项和Sn。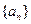 的各项均为正数,
的各项均为正数,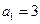 ,前
,前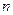 项和为
项和为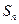 ,
,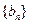 为等比数列,
为等比数列, 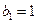 ,且
,且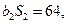
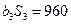 .
.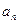 与
与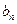 ;(2)求和:
;(2)求和: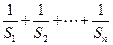 .
. 中,第2、3、7项成等比数列,求公比q.
中,第2、3、7项成等比数列,求公比q.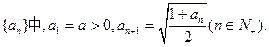
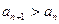 恒成立;
恒成立;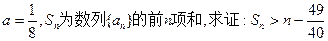 ;
;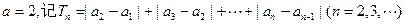 ,求证:
,求证: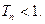
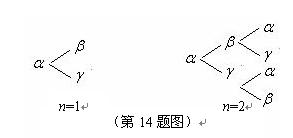
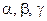 三个字母组成一个长度为
三个字母组成一个长度为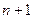
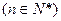 个字母的字符串,要求由
个字母的字符串,要求由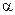 开始,相邻两个字母不同. 例如
开始,相邻两个字母不同. 例如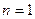 时,排出的字符串可能是
时,排出的字符串可能是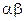 或
或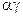 ;
;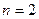 时排出的字符串可能是
时排出的字符串可能是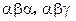
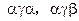 (如图).若记长度为
(如图).若记长度为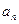 ,
,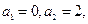 则数列
则数列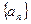 的前
的前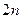 项之和为 .
项之和为 .