题目内容
等差数列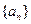 的各项均为正数,
的各项均为正数,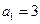 ,前
,前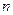 项和为
项和为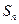 ,
,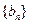 为等比数列,
为等比数列, 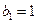 ,且
,且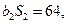
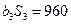 .
.
(1)求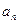 与
与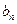 ;(2)求和:
;(2)求和: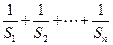 .
.
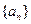 的各项均为正数,
的各项均为正数,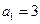 ,前
,前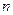 项和为
项和为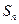 ,
,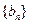 为等比数列,
为等比数列, 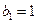 ,且
,且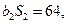
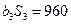 .
.(1)求
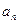 与
与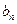 ;(2)求和:
;(2)求和: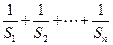 .
.(1)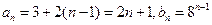
(2)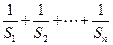 .
.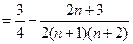
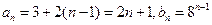
(2)
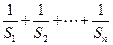 .
.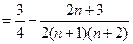
(1)设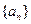 的公差为
的公差为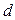 ,
,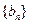 的公比为
的公比为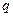 ,则
,则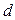 为正整数,
为正整数,
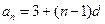 ,
,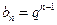
依题意有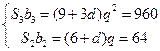 ①
①
解得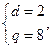 或
或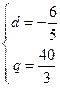 (舍去)
(舍去)
故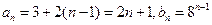
(2)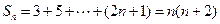
∴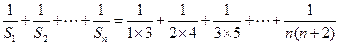
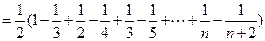
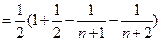
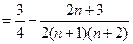
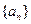 的公差为
的公差为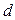 ,
,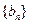 的公比为
的公比为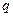 ,则
,则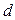 为正整数,
为正整数,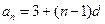 ,
,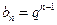
依题意有
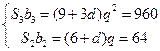 ①
①解得
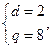 或
或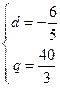 (舍去)
(舍去) 故
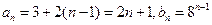
(2)
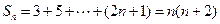
∴
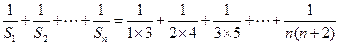

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
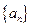 :
: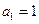 ,
,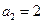 ,
,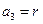 ,
,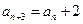 (
(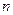 是正整数),与数列
是正整数),与数列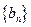 :
: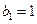 ,
,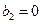 ,
,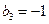 ,
,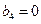 ,
,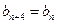 (
(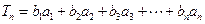 .
.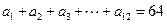 ,求
,求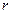 的值;
的值;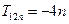 ;
;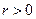 ,且存在正整数
,且存在正整数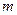 ,使得在
,使得在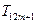 ,
,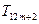 ,
,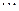 ,
,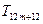 中有4项为100.
中有4项为100.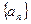 中,若
中,若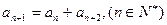 ,则称数列
,则称数列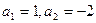 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;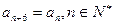 ;
;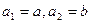 ,若数列
,若数列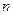 项和
项和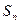 。
。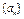 满足
满足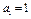 ,
,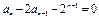 ,(
,(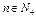 ,
,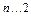 ).
).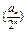 是等差数列;
是等差数列;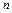 项和为
项和为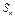 ,且
,且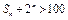 恒成立,求
恒成立,求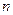 满足以下运算性质:
满足以下运算性质: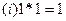 ,
,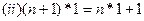 ,求
,求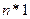
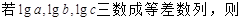 ( )
( )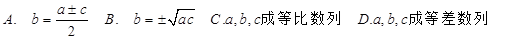
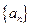 满足:
满足: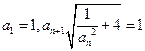 ,记
,记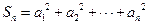 ,若
,若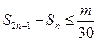 对任意的
对任意的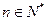 恒成立,则正整数
恒成立,则正整数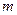 的最小值为 .
的最小值为 .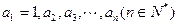 的法则如下:如果
的法则如下:如果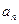 为自然数,则写
为自然数,则写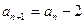 ,否则就写
,否则就写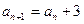 ,则
,则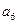 =_____。(注意:0是自然数)
=_____。(注意:0是自然数)
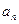
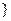 的前
的前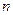 项和为
项和为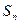 ,点列
,点列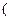
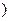 在函数
在函数
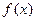 =
=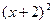 的图像上.数列
的图像上.数列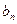
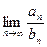 =2成立,则数列
=2成立,则数列