题目内容
12．已知函数f（x）=ax3-bx+4，f（1）=7，则f（-1）=1．分析 直接利用函数的解析式以及函数的奇偶性，求解函数值即可．
解答 解：函数f（x）=ax3-bx+4满足f（1）=7，
即：f（1）=a-b+4=7，a-b=3，
则f（-1）=-a+b+4=-3+4=1．
故答案为：1．
点评 本题考查函数的值的求法，考查计算能力．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
3．已知焦点在x轴上，长、短半轴之和为10，焦距为4$\sqrt{5}$，则椭圆的方程为（ ）
| A． | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{36}$=1 | C． | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1 | D． | $\frac{{y}^{2}}{6}$+$\frac{{x}^{2}}{4}$=1 |
20．已知数列的通项公式an=n（n-3），则180是它的第（ ）项．
| A． | -12 | B． | -15 | C． | 12 | D． | 15 |
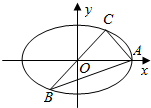已知A、B、C是椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的三点，其中A的坐标为（2$\sqrt{3}$，0），BC过椭圆E的中心，且椭圆长轴的一个端点与短轴的两个端点构成正三角形．