题目内容
12．已知R为实数集，集合A={x|x2≥4}，B={y|y=|tanx|}，则（∁RA）∩B=（ ）| A． | {x|x≤2} | B． | {x|x＞0} | C． | {x|0≤x＜2} | D． | {x|0＜x＜2} |
分析 先求出x2≥4的解集可得集合B，由补集的运算求出∁RA，由正切函数的值域求出B，再由交集的运算求出（∁RA）∩B．
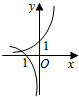
解答 解：由x2≥4得x≥2或x≤-2，则A={x|x≥2或x≤-2}，
∴∁RA={x|-2＜x＜2}，
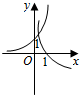
∵B={y|y=|tanx|}={y|y≥0}，∴（∁RA）∩B={x|0≤x＜2}，
故选：C．
点评 本题考查交、并、补集的混合运算，一元二次不等式的解法，以及正切函数的值域，属于基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
3．不等式x2-3x-4＞0的解集为（ ）
| A． | {x|x＜-1或x＞4} | B． | {x|x≤-1或x≥4} | C． | {x|-1＜x＜4} | D． | {x|-1≤x≤4} |
20．已知a∈R，复数z=$\frac{n-i}{1-i}$是纯虚数（i是虚数单位），则a=（ ）
| A． | -$\sqrt{2}$ | B． | -1 | C． | 1 | D． | $\sqrt{2}$ |
4．小吴同学计划大学毕业后出国留学，其父母于2014年7月1日在银行存入a元钱，此后每年7月1日存入a元钱，若年利润为p且保持不变，并约定每年到期，存款的本息均自动转为新的一年的定期，在小吴同学2019年7月1日大学毕业时取出这五笔存款，则可以取出的钱（元）的总数为（ ）
| A． | a（1+p）5 | B． | a（1+p）6 | C． | $\frac{a}{p}$[（1+p）5-（1+p）] | D． | $\frac{a}{p}$[（1+p）6-（1+p）] |
1．已知a∈R，复数z=$\frac{a-i}{1-i}$是纯虚数（i数虚数单位），则a=（ ）
| A． | $-\sqrt{2}$ | B． | -1 | C． | 1 | D． | $\sqrt{2}$ |