题目内容
4.小吴同学计划大学毕业后出国留学,其父母于2014年7月1日在银行存入a元钱,此后每年7月1日存入a元钱,若年利润为p且保持不变,并约定每年到期,存款的本息均自动转为新的一年的定期,在小吴同学2019年7月1日大学毕业时取出这五笔存款,则可以取出的钱(元)的总数为( )| A. | a(1+p)5 | B. | a(1+p)6 | C. | $\frac{a}{p}$[(1+p)5-(1+p)] | D. | $\frac{a}{p}$[(1+p)6-(1+p)] |
分析 先分别计算每一年存入a元到2019年的本息和,然后将所有存款的本息相加,由等比数列求得求和公式可得
解答 解:2014年的a元到了2019年本息和为a(1+q)5,
2015年的a元到了2019年本息和为a(1+q)4,
2016年的a元到了2019年本息和为a(1+q)3,
所有金额为a(1+q)+a(1+q)2+…+a(1+q)5=$\frac{a(1+p)[1-(1+p)^{5}]}{1-(1+p)}$=$\frac{a}{p}$[(1+p)6-(1+p)],
故选:D
点评 本题考查等比数列,涉及数列的应用和等比数列的求和公式,属中档题

练习册系列答案
相关题目
12.已知R为实数集,集合A={x|x2≥4},B={y|y=|tanx|},则(∁RA)∩B=( )
| A. | {x|x≤2} | B. | {x|x>0} | C. | {x|0≤x<2} | D. | {x|0<x<2} |
16.在面积为1的△ABC内部随机选取一点P,则△PBC面积大于$\frac{1}{4}$的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{9}{16}$ |
13.复数z=$\frac{2i-1}{(1-i)^{2}}$=( )
| A. | 1+$\frac{1}{2}$i | B. | -1+$\frac{1}{2}$i | C. | -1-$\frac{1}{2}$i | D. | 1-$\frac{1}{2}$i |
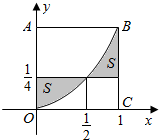 在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.
在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.