题目内容
6.定义运算a*b为执行如图所示的程序框图输出的S值,则$(cos\frac{5π}{12})*(sin\frac{5π}{12})$的值为$\frac{1}{2}$.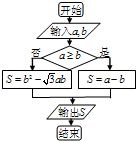
分析 由已知的程序框图可知:本程序的功能是:计算并输出分段函数S=$\left\{\begin{array}{l}{a-b}&{a≥b}\\{{b}^{2}-\sqrt{3}ab}&{a<b}\end{array}\right.$的值,由已知计算出a,b的值,代入可得答案.
解答 解:由已知的程序框图可知:
本程序的功能是:计算并输出分段函数S=$\left\{\begin{array}{l}a-b,&a≥b\\{b}^{2}-\sqrt{3}ab,&a<b\end{array}\right.$的值,
∵a=cos$\frac{5π}{12}$<b=sin$\frac{5π}{12}$,
∴S=sin2$\frac{5π}{12}$-$\sqrt{3}×$cos$\frac{5π}{12}$×sin$\frac{5π}{12}$
=$\frac{1}{2}$-($\frac{1}{2}$cos$\frac{5π}{6}$+$\frac{\sqrt{3}}{2}$sin$\frac{5π}{6}$)
=$\frac{1}{2}$-sinπ
=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查的知识点是程序框图,特殊角的三角函数,其中根据已知的程序框图,分析出程序的功能是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.对于定义在R上的函数f(x),若存在x0使得$\underset{\underbrace{f(f…(f({x}_{0})))}}{k}$=x0(*),其中k为某个正整数,则称x0为函数f(x)的一个周期点,使得(*)式成立的正整数k称为x0的周期,使得(*)式成立的最小正整数k称为x0的最小周期,若函数f(x)=1-|2x-1|,则函数f(x)( )
| A. | 恰有一个最小周期为1的周期点,恰有一个最小周期为2的周期点 | |
| B. | 恰有一个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| C. | 恰有两个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| D. | 恰有两个最小周期为1的周期点,恰有四个最小周期为2的周期点 |
1.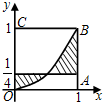 如图,正方形OABC的边长为1,记曲线y=x2和直线$y=\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)为Ω,若向正方形OABC内任意投一点M,则点M落在区域Ω内的概率为( )
如图,正方形OABC的边长为1,记曲线y=x2和直线$y=\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)为Ω,若向正方形OABC内任意投一点M,则点M落在区域Ω内的概率为( )
 如图,正方形OABC的边长为1,记曲线y=x2和直线$y=\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)为Ω,若向正方形OABC内任意投一点M,则点M落在区域Ω内的概率为( )
如图,正方形OABC的边长为1,记曲线y=x2和直线$y=\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)为Ω,若向正方形OABC内任意投一点M,则点M落在区域Ω内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
11.复数$\frac{3+2i}{1-i}$=( )
| A. | $\frac{1}{2}+\frac{5}{2}i$ | B. | $\frac{1}{2}-\frac{5}{2}i$ | C. | $-\frac{1}{2}+\frac{5}{2}i$ | D. | $-\frac{1}{2}-\frac{5}{2}i$ |
18.已知复数z=1+i+i2+…i10,则复数z在复平面内对应的点为( )
| A. | (1,1) | B. | (1,-1) | C. | (0,1) | D. | (1,0) |
15.点P在直径为5的球面上,过P作两两互相垂直的三条弦(两端点均在球面上的线段),若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| A. | 2$\sqrt{14}$ | B. | 2$\sqrt{70}$ | C. | $\sqrt{70}$ | D. | $\sqrt{14}$ |