题目内容

【题目】如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．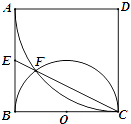
（1）求证：AE=EB；
（2）求EFFC的值．

【答案】
（1）证明：由以D为圆心DA为半径作圆，

而ABCD为正方形，∴EA为圆D的切线

依据切割线定理，得EA2=EFEC

另外圆O以BC为直径，∴EB是圆O的切线，

同样依据切割线定理得EB2=EFEC

故AE=EB


（2）解：连结BF，

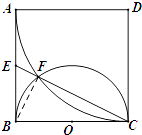
∵BC为圆O直径，

∴BF⊥EC

在RT△EBC中，有

又在Rt△BCE中，

由射影定理得EFFC=BF2= ．


【解析】（1）由题意得EA为圆D的切线，由切割线定理，得EA2=EFEC，EB2=EFEC，由此能证明AE=EB．（2）连结BF，得BF⊥EC，在RT△EBC中， ，由射影定理得EFFC=BF2 ， 由此能求出结果．

练习册系列答案
相关题目

【题目】设x，y∈R，则（3﹣4y﹣cosx）2+（4+3y+sinx）2的最小值为（ ）
A.4
B.5
C.16
D.25

【题目】如图，已知平面 平面， 与分别是棱长为1与2的正三角形， // ，四边形为直角梯形， // ， ，点为的重心， 为中点， .

（Ⅰ）当时，求证： //平面；

（Ⅱ）若直线与所成角为，试求二面角的余弦值.

【题目】已知 分别为椭圆的左、右焦点，椭圆离心率，直线通过点,且倾斜角是45°.

(1)求椭圆的标准方程；

(2)若直线与椭圆交于两点，求的面积.

【题目】设函数f（x）=x3+ax2+bx（x＞0）的图像与x轴相切于M（3，0）．
（1）求f（x）的解析式；
（2）是否存在两个不等正数s，t（s＜t），当x∈[s，t]时，函数f（x）=x3+ax2+bx的值域也是[s，t]，若存在，求出所有这样的正数s，t，若不存在，请说明理由．

【题目】在直角坐标系中，以原点为极点， 轴的正半轴为极轴，以相同的长度单位建立极坐标系，已知直线的极坐标方程为，曲线的极坐标方程为.

（1）设为参数，若，求直线的参数方程；

（2）已知直线与曲线交于，设，且，求实数的值.

【题目】如图，有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知且设，绿地面积为.

(1)写出关于的函数关系式，并指出这个函数的定义域．

(2)当为何值时，绿地面积最大？

【题目】在△ABC中，a，b，c分别为A，B，C所对边，a+b=4，（2﹣cosA）tan =sinA．
（1）求边长c的值；
（2）若E为AB的中点，求线段EC的范围．

【题目】已知抛物线的顶点是坐标原点，焦点在轴的正半轴上，过焦点且斜率为的直线与抛物线交于两点，且满足.

（1）求抛物线的方程；

（2）已知为抛物线上一点，若点位于轴下方且，求的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网