Question

【题目】设x，y∈R，则（3﹣4y﹣cosx）2+（4+3y+sinx）2的最小值为（ ）
A.4
B.5
C.16
D.25

Answer 1

【答案】C
【解析】解：∵（3﹣4y﹣cosx）2+（4+3y+sinx）2= ，类比两点间的距离公式|AB|= ，
而且3（3﹣4y）+4（4+3y）﹣25=0，
∴所求的式子为直线3x+4y﹣25=0上的一点到圆x2+y2=1上的一点的距离的平方，
画图可知，过原点O（0，0）作3x+4y﹣25=0的垂线段，垂足为P，|OP|= =5，
OP与圆的交点分别为M、N，
显然，（3﹣4y﹣cosx）2+（4+3y+sinx）2的最小值为|PM|2=（|OP|﹣|OM|）2=（|OP|﹣1）2=16．
故选C．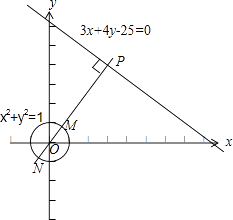

【考点精析】解答此题的关键在于理解三角函数的最值的相关知识，掌握函数，当时，取得最小值为；当时，取得最大值为，则，，．