题目内容
【题目】设函数f(x)=x3+ax2+bx(x>0)的图像与x轴相切于M(3,0).
(1)求f(x)的解析式;
(2)是否存在两个不等正数s,t(s<t),当x∈[s,t]时,函数f(x)=x3+ax2+bx的值域也是[s,t],若存在,求出所有这样的正数s,t,若不存在,请说明理由.
【答案】
(1)解:f′(x)=3x2+2ax+b,依题意有  ,
,
即 ![]() ,解得
,解得 ![]() .
.
∴f(x)=x3﹣6x2+9x
(2)解:f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3),
由f′(x)=0,得x=1或x=3.
当x∈(﹣∞,1),(3,+∞)时,f′(x)>0,函数为增函数,
当x∈(1,3)时,f′(x)<0,函数为减函数,
∴f(x)=x3﹣6x2+9x的极大值为4,极小值为0.
①若极值点3在[s,t]上,
∵函数的值域也是[s,t],
∴0∈[s,t],这与s>0矛盾;
②若极值点1在[s,t]上,
∵函数的值域也是[s,t],
∴4∈[s,t],这与0<s≤1≤t<3矛盾;
③若f(x)=x3﹣6x2+9x在区间[s,t]上单调递增,
即0<s<t<1或3<s<t,则 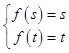 ,
,
即s,t是方程x3﹣6x2+9x=x的两个不同正根,解得 ![]() 舍去;
舍去;
④若f(x)=x3﹣6x2+9x在区间[s,t]上单调递减,
即1≤s<t≤3,则 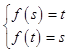 ,
,
两式相减并除以s﹣t得:(s+t)2﹣6(s+t)﹣st+10=0*,
两式相除并开方可得:s(s﹣3)=t(t﹣3),
∴s+t=3.代入*得st=1.
∴s,t为方程x2﹣3x+1=0的两根,
解得: ![]() .
.
综上,存在 ![]() 满足条件
满足条件
【解析】(1)由已知得f′(x)=3x2+2ax+b.依题意f(3)=0,f′(3)=0,解方程即可求出f(x)=x3﹣6x2+9x; (2)由函数的定义域是正数知,s>0,故极值点x=3不在区间[s,t]上,由此利用分类讨论思想能求出不存在正数s,t满足要求.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】为了调查每天微信用户使用微信的时间,某经销化妆品分微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |