题目内容
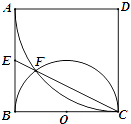
【题目】如图,已知平面![]()
![]() 平面
平面![]() ,
, ![]() 与
与![]() 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, ![]() //
// ![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() //
// ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)借助题设条件运用线面平行的判定定理推证;(2)借助题设运用空间向量的数量积公式探求.
试题解析:
解:(Ⅰ)连![]() 延长交
延长交![]() 于
于![]() ,
,
因为点![]() 为
为![]() 的重心,所以
的重心,所以![]()
又![]() ,所以
,所以![]() ,所以
,所以![]() //
// ![]() ;
;
因为![]() //
// ![]() ,
, ![]() //
// ![]() ,所以平面
,所以平面![]() //平面
//平面![]() ,
,
又![]() 与
与![]() 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,
![]() 为
为![]() 中点,
中点, ![]() 为
为![]() 中点,
中点, ![]() //
// ![]() ,又
,又![]() //
// ![]() ,
,
所以![]() //
// ![]() ,得
,得![]() 四点共面
四点共面
![]() //平面
//平面![]()
(Ⅱ)平面![]()
![]() 平面
平面![]() ,易得平面
,易得平面![]()
![]() 平面
平面![]() ,
,
以![]() 为原点,
为原点, ![]() 为x轴,
为x轴, ![]() 为y轴,
为y轴, ![]() 为z轴建立空间直角坐标系,
为z轴建立空间直角坐标系,
则 ,设
,设![]() ,
,
![]()
 ,
, 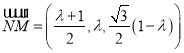 ,
, ![]()
因为![]() 与
与![]() 所成角为
所成角为![]() ,所以
,所以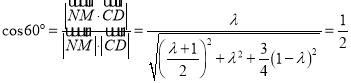 ,
,
得![]() ,
, ![]() ,
, 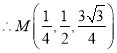 ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则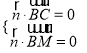 ,取
,取![]() ,
,
面![]() 的法向量
的法向量![]() ,所以二面角
,所以二面角![]() 的余弦值
的余弦值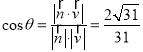 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了调查每天微信用户使用微信的时间,某经销化妆品分微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |