题目内容
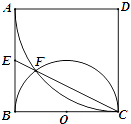
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知![]() 且
且![]() 设
设![]() ,绿地面积为
,绿地面积为![]() .
.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出这个函数的定义域.
的函数关系式,并指出这个函数的定义域.
(2)当![]() 为何值时,绿地面积
为何值时,绿地面积![]() 最大?
最大?

【答案】(1)∴y=-2x2+(a+2)x,0<x≤2
(2)当![]() 时,AE=
时,AE=![]() 时,绿地面积取最大值
时,绿地面积取最大值![]() ;
;
当a≥6时,AE=2时,绿地面积取最大值2a-4
【解析】
解:(1)SΔAEH=SΔCFG=![]() x2,SΔBEF=SΔDGH=
x2,SΔBEF=SΔDGH=![]() (a-x)(2-x). ……1分
(a-x)(2-x). ……1分
∴y=SABCD-2SΔAEH-2SΔBEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x. ……3分
由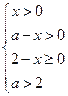 ,得
,得![]()
∴y=-2x2+(a+2)x,其定义域为![]() . ……4分
. ……4分
(2)当![]() ,即a<6时,则x=
,即a<6时,则x=![]() 时,y取最大值
时,y取最大值![]() . ……6分
. ……6分
当![]() ≥2,即a≥6时,y=-2x2+(a+2)x,在
≥2,即a≥6时,y=-2x2+(a+2)x,在![]() 0,2]上是增函数,则x=2时,y取最大值2a-4 . ……8分
0,2]上是增函数,则x=2时,y取最大值2a-4 . ……8分
综上所述:当a<6时,AE=![]() 时,绿地面积取最大值
时,绿地面积取最大值![]() ;当a≥6时,AE=2时,绿地面积取最大值2a-4.
;当a≥6时,AE=2时,绿地面积取最大值2a-4.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】为了调查每天微信用户使用微信的时间,某经销化妆品分微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |