Question

【题目】在直角坐标系中，以原点为极点， 轴的正半轴为极轴，以相同的长度单位建立极坐标系，已知直线的极坐标方程为，曲线的极坐标方程为.

（1）设为参数，若，求直线的参数方程；

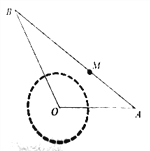
（2）已知直线与曲线交于，设，且，求实数的值.

Answer 1

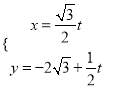【答案】(1) （为参数）；(2) .

【解析】试题分析：（1）利用直线极坐标方程和直角坐标方程互化的公式，先得直角坐标方程，再根据，即可求直线l参数方程；（2）把直线l的参数方程代入曲线C的方程，设MP=t1，MQ=t2．根据|PQ|2=|MP||MQ|， 根据根与系数的关系即可得出．

解析：（1）直线的极坐标方程为

所以，即

因为为参数，若，代入上式得，

所以直线的参数方程为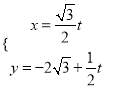（为参数）

（2）由，得

由代入，得

将直线的参数方程与的直角坐标方程联立

得（*）

，

设点分别对应参数恰为上述方程的根

则，

由题设得，

则有，得或

因为，所以.