Question

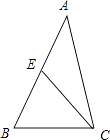
【题目】在△ABC中，a，b，c分别为A，B，C所对边，a+b=4，（2﹣cosA）tan =sinA．
（1）求边长c的值；
（2）若E为AB的中点，求线段EC的范围．

Answer 1

【答案】
（1）解：在△ABC中，∵（2﹣cosA）tan =sinA，a+b=4，

∴（2﹣cosA） =sinA，

即2sinC=sinA+sinAcosC+cosAsinC=sinA+sinB，

∴由正弦定理可得：2c=a+b=4，

∴c=2．

（2）解：∵c=2，E为AB的中点，

∴由余弦定理可得：CE2=AE2+AC2﹣2AEACcosA=a2+1﹣2acosB，

CE2=BE2+BC2﹣2BEBCcosB=b2+1﹣2bcosA，

∴两式相加可得：CE2= ，

又∵cosB= ，cosA= ，a=4﹣b，

∴ ，

又∵ ，

∴1＜b＜3，

∴ ．

【解析】（1）使用半角公式化简条件式，利用正弦定理结合已知即可得解c的值．（2）利用已知及余弦定理可得 ，又结合 ，可得b的范围，利用二次函数的性质即可解得CE的范围．