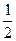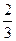题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn(n∈N*).
(1)求数列{an}的通项an;
(2)求数列{nan}的前n项和Tn.
(1)求数列{an}的通项an;
(2)求数列{nan}的前n项和Tn.
(1)∵an+1=2Sn,∴Sn+1-Sn=2Sn,∴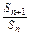 =3.
=3.
又∵S1=a1=1,
∴数列{Sn}是首项为1、公比为3的等比数列,
Sn=3n-1(n∈N*).
当n≥2时,an=2Sn-1=2·3n-2(n≥2),
∴an=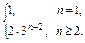
(2)Tn=a1+2a2+3a3+…+nan.
当n=1时,T1=1;
当n≥2时,Tn=1+4·30+6·31+…+2n·3n-2, ①
3Tn=3+4·31+6·32+…+2n·3n-1, ②
①-②得:
-2Tn=-2+4+2(31+32+…+3n-2)-2n·3n-1
=2+2·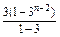 -2n·3n-1
-2n·3n-1
=-1+(1-2n)·3n-1.
∴Tn=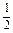 +
+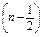 ·3n-1(n≥2).
·3n-1(n≥2).
又∵T1=a1=1也满足上式,
∴Tn=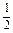 +3n-1(n-
+3n-1(n-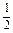 ) (n∈N*).
) (n∈N*).
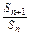 =3.
=3.又∵S1=a1=1,
∴数列{Sn}是首项为1、公比为3的等比数列,
Sn=3n-1(n∈N*).
当n≥2时,an=2Sn-1=2·3n-2(n≥2),
∴an=
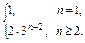
(2)Tn=a1+2a2+3a3+…+nan.
当n=1时,T1=1;
当n≥2时,Tn=1+4·30+6·31+…+2n·3n-2, ①
3Tn=3+4·31+6·32+…+2n·3n-1, ②
①-②得:
-2Tn=-2+4+2(31+32+…+3n-2)-2n·3n-1
=2+2·
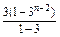 -2n·3n-1
-2n·3n-1=-1+(1-2n)·3n-1.
∴Tn=
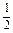 +
+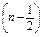 ·3n-1(n≥2).
·3n-1(n≥2).又∵T1=a1=1也满足上式,
∴Tn=
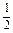 +3n-1(n-
+3n-1(n-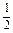 ) (n∈N*).
) (n∈N*).
练习册系列答案
相关题目

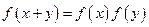
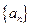 满足
满足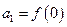 ,且
,且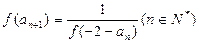 ,数列
,数列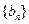 满足
满足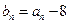
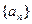 满足
满足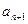 ≤
≤ . (1)若
. (1)若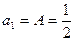 ,
,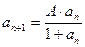 时,求
时,求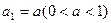 ,A=1,证明:
,A=1,证明: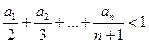
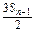 总成等差数列.
总成等差数列. =an(Sn-
=an(Sn-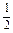 ).
).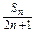 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.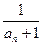 }为等差数列,则a11等于( )
}为等差数列,则a11等于( )