题目内容
已知数列{an}中,a1=1,当n≥2时,其前n项和Sn满足S =an(Sn-
=an(Sn-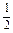 ).
).
(1)求Sn的表达式;
(2)设bn=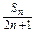 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
 =an(Sn-
=an(Sn-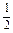 ).
).(1)求Sn的表达式;
(2)设bn=
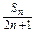 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.(1)Sn=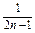 (2)Tn=
(2)Tn=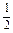
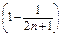 =
=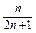 .
.
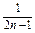 (2)Tn=
(2)Tn=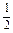
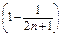 =
=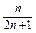 .
. (1)∵S =an
=an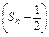 ,an=Sn-Sn-1,(n≥2),
,an=Sn-Sn-1,(n≥2),
∴S =(Sn-Sn-1)
=(Sn-Sn-1)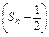 ,
,
即2Sn-1Sn=Sn-1-Sn, ① 4分
由题意Sn-1·Sn≠0,
①式两边同除以Sn-1·Sn,得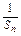 -
-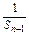 =2,
=2,
∴数列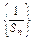 是首项为
是首项为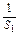 =
=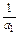 =1,
=1,
公差为2的等差数列. 6分
∴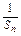 =1+2(n-1)=2n-1,∴Sn=
=1+2(n-1)=2n-1,∴Sn=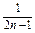 . 8分
. 8分
(2)又bn=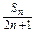 =
=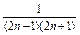
=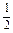
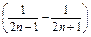 , 10分
, 10分
∴Tn=b1+b2+…+bn
=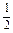
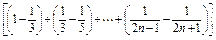
=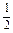
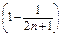 =
=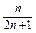 . 14分
. 14分
 =an
=an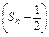 ,an=Sn-Sn-1,(n≥2),
,an=Sn-Sn-1,(n≥2),∴S
 =(Sn-Sn-1)
=(Sn-Sn-1)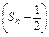 ,
,即2Sn-1Sn=Sn-1-Sn, ① 4分
由题意Sn-1·Sn≠0,
①式两边同除以Sn-1·Sn,得
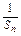 -
-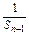 =2,
=2,∴数列
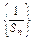 是首项为
是首项为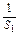 =
=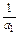 =1,
=1,公差为2的等差数列. 6分
∴
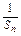 =1+2(n-1)=2n-1,∴Sn=
=1+2(n-1)=2n-1,∴Sn=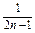 . 8分
. 8分(2)又bn=
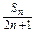 =
=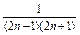
=
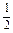
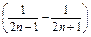 , 10分
, 10分∴Tn=b1+b2+…+bn
=
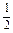
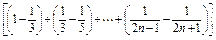
=
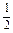
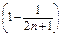 =
=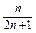 . 14分
. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
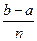
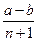

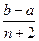
 北黄冈中学·
北黄冈中学·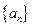 满足
满足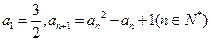 ,求
,求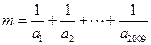 的
的 整数部分。
整数部分。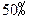 .每年年底扣除下一年的消费基金后,余下的资金投入再生产.这家牛奶厂每年应扣除多少消费基金,才能实现经过5年资金达到2000万元的目标?
.每年年底扣除下一年的消费基金后,余下的资金投入再生产.这家牛奶厂每年应扣除多少消费基金,才能实现经过5年资金达到2000万元的目标?