题目内容
已知数列{an}中,a1=1,前n项和为Sn,对任意的n≥2,3Sn-4,an,2- 总成等差数列.
总成等差数列.
(1)求a2、a3、a4的值;
(2)求通项公式an.
 总成等差数列.
总成等差数列.(1)求a2、a3、a4的值;
(2)求通项公式an.
(1)a2= ,a3=-
,a3=-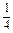 ,a4=
,a4= .(2)an=
.(2)an=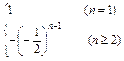 .
.
 ,a3=-
,a3=-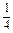 ,a4=
,a4= .(2)an=
.(2)an=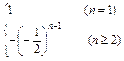 .
.(1)当n≥2时,3Sn-4,an,2- 成等差数列,
成等差数列,
∴2an=3Sn-4+2- Sn-1,∴an=3Sn-4(n≥2).
Sn-1,∴an=3Sn-4(n≥2).
由a1=1,得a2=3(1+a2)-4,
∴a2= ,a3=3
,a3=3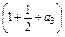 -4,
-4,
∴a3=-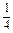 ,a4=3
,a4=3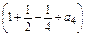 -4,∴a4=
-4,∴a4= .
.
∴a2= ,a3=-
,a3=-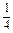 ,a4=
,a4= .
.
(2)∵当n≥2时,an=3Sn-4,∴3Sn=an+4,
∴ ,可得:3an+1=an+1-an,
,可得:3an+1=an+1-an,
∴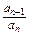 =-
=- ,∴a2,a3,…,an成等比数列,
,∴a2,a3,…,an成等比数列,
∴an=a2·qn-2= ·
·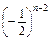 =-
=-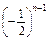 ,
,
∴an=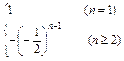 .
.
 成等差数列,
成等差数列,∴2an=3Sn-4+2-
 Sn-1,∴an=3Sn-4(n≥2).
Sn-1,∴an=3Sn-4(n≥2).由a1=1,得a2=3(1+a2)-4,
∴a2=
 ,a3=3
,a3=3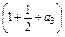 -4,
-4,∴a3=-
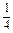 ,a4=3
,a4=3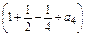 -4,∴a4=
-4,∴a4= .
.∴a2=
 ,a3=-
,a3=-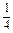 ,a4=
,a4= .
.(2)∵当n≥2时,an=3Sn-4,∴3Sn=an+4,
∴
 ,可得:3an+1=an+1-an,
,可得:3an+1=an+1-an,∴
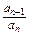 =-
=- ,∴a2,a3,…,an成等比数列,
,∴a2,a3,…,an成等比数列,∴an=a2·qn-2=
 ·
·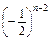 =-
=-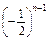 ,
,∴an=
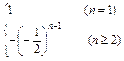 .
.
练习册系列答案
相关题目
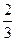 ,且
,且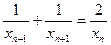 (n≥2),则xn等于( )
(n≥2),则xn等于( )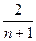
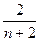
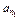 ,
,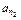 ,…,
,…,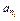 ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式. 的前n项和,求Tn.
的前n项和,求Tn.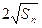 =an+1.
=an+1.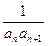 ,求数列{bn}的前n项和Bn.
,求数列{bn}的前n项和Bn.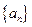 的公差
的公差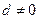 ,记
,记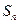 为数列
为数列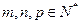 ,且
,且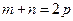 ,则
,则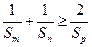 ;
;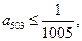 则
则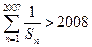 。
。