题目内容
已知等差数列{an}的公差为1,且a1+a2+a3+…+a99=99,则a3+a6+a9+…+a99的值是多少?
由已知a1+a2+a3+…+a99=99,
有99a1+(1+2+…+98)=99,
99a1+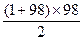 -99=0,
-99=0,
∴99(a1+48)=0.
∴a1=-48,d=1.
∴a3+a6+a9+…+a99=a3+(a3+3)+(a3+6)+…+[a3+(33-1)×3]
=33a3+3(1+2+3+…+32)=33a3+3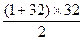 =33(-46+48)=66.
=33(-46+48)=66.
有99a1+(1+2+…+98)=99,
99a1+
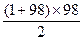 -99=0,
-99=0,∴99(a1+48)=0.
∴a1=-48,d=1.
∴a3+a6+a9+…+a99=a3+(a3+3)+(a3+6)+…+[a3+(33-1)×3]
=33a3+3(1+2+3+…+32)=33a3+3
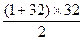 =33(-46+48)=66.
=33(-46+48)=66.所谓整体处理,就是指从整体角度思考问题,表现在解题时把一些组合式子或把解题过程当作一个整体来考虑的解题方法.可由已知式出发求得a1,又已知公差d,所以可求得a3,这样在首项a3,公差d已知的条件下,就可求被求式的值了.

练习册系列答案
相关题目
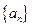 的各项均为正数,观察下面程序框图,当
的各项均为正数,观察下面程序框图,当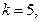
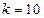 时,分别
时,分别
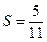 和
和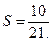 .
.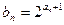 ,
,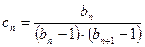
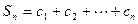 求证:
求证: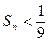 .
.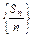 为等比数列;
为等比数列;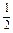 ,
,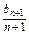 =
=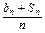 (n∈N*),求数列{bn}的通项公式.
(n∈N*),求数列{bn}的通项公式. 北黄冈中学·
北黄冈中学·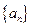 满足
满足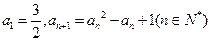 ,求
,求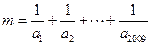 的
的 整数部分。
整数部分。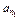 ,
,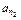 ,…,
,…,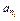 ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式.