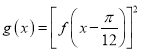题目内容
【题目】我国古代数学家祖暅提出原理：“幂势既同，则积不容异”.其中“幂”是截面积，“势”是几何体的高.原理的意思是：夹在两个平行平面间的两个几何体，被任一平行于这两个平行平面的平面所截，若所截的两个截面的面积恒相等，则这两个几何体的体积相等.如图所示，在空间直角坐标系
的坐标平面
内，若函数
的图象与
轴围成一个封闭区域
，将区域沿
轴的正方向上移4个单位，得到几何体如图一.现有一个与之等高的圆柱如图二，其底面积与区域面积相等，则此圆柱的体积为__________．
【答案】
【解析】分析：首先确定底面积，然后结合柱体的体积公式整理计算即可求得最终结果.
详解：由题意可知，图一中底面积是由一个四分之一圆与一个直角三角形组成的图形，
由
可知，该四分之一圆的半径为2，其面积为：
,
由
，令
可得
，由
可得
，
则直角三角形与坐标轴的交点坐标为
，
，
直角三角形的面积
，
结合题意可得：区域A的面积，即圆柱的底面积：
，
结合祖暅原理可得，此圆柱的体积
.
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
