��Ŀ����
����Ŀ��ijУ�����˶��ᣬ����������Զ�ijɼ���8.0�� (��������,��ȷ��0.1��) ���ϵĽ�����������������ݽ��������ֳ�6�黭��Ƶ�ʷֲ�ֱ��ͼ��һ����(��ͼ)����֪������ǰ5��С���Ƶ�ʷֱ�Ϊ0.04��0.10��0.14��0.28��0.30 ����6С���Ƶ����7 .

��������������������
�������Ӹ�Уѧ���������ࣩܶ�������ȡ��������![]() ��ʾ�����н����������������
��ʾ�����н����������������![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
(��) ������β��Ժ��֣��׳ɼ����ȷֲ���8��10��֮�䣬�ҳɼ����ȷֲ���9.5��10.5��֮�䣬�ּ�,�Ҹ���һ�Σ���ױ���Զ�ĸ���.
���𰸡�����![]() ; ����������(��)
; ����������(��)![]() .
.
��������
����������������������е�Ƶ�ʷֲ�ֱ��ͼ��Ƶ�ʺ�Ƶ��֮��Ĺ�ϵ���; ���������������ñ�Ŭ����ʷֲ���ʽ̽��(��)![]() �������ùŵ����ʽ���:
�������ùŵ����ʽ���:
����6С���Ƶ��Ϊ1��(0.04��0.10��0.14��0.28��0.30)��0.14��
��������Ϊ![]() (��). ��������������������������������������������������2��
(��). ��������������������������������������������������2��
���4��5��6��ɼ����������������Ϊ(0.28��0.30��0.14)��50��36(��)
���������������Ϊ![]() . ��������������������������������������������������4��
. ��������������������������������������������������4��
����![]() =0,1,2,��������ĸ���Ϊ
=0,1,2,��������ĸ���Ϊ![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() .������������������������6�֡�����������
.������������������������6�֡�����������
����ֲ���Ϊ

![]() �������н����������������ѧ����Ϊ
�������н����������������ѧ����Ϊ![]() . ������������������8��
. ������������������8��
(��)��ס��Ҹ���һ�εijɼ��ֱ�Ϊ![]() �ף�������¼����������Ϊ
�ף�������¼����������Ϊ
![]() ��
��
�¼�![]() ���ױ���Զ�ĸ��ʡ����������Ϊ
���ױ���Զ�ĸ��ʡ����������Ϊ![]() ����ͼ��ʾ. ��������������������10��
����ͼ��ʾ. ��������������������10��

���ɼ��θ���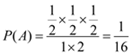 . ���ױ���Զ�ĸ���Ϊ
. ���ױ���Զ�ĸ���Ϊ![]() .����������������12��
.����������������12��









