题目内容
【题目】由无理数论引发的数字危机一直延续到19世纪，直到1872年，德国数学家戴德金从连续性的要求出发，用有理数的“分割”来定义无理数（史称戴德金分割），并把实数理论建立在严格的科学基础上，才结束了无理数被认为“无理”的时代，也结束了持续2000多年的数学史上的第一次大危机，所谓戴德金分割，是指将有理数集
划分为两个非空的子集
与
，且满足
，
，中的每一个元素都小于中的每一个元素，则称
为戴德金分割.试判断，对于任一戴德金分割，下列选项中，可能成立的是____．
①没有最大元素，有一个最小元素；②没有最大元素，也没有最小元素；
③有一个最大元素，有一个最小元素；④有一个最大元素，没有最小元素.
【答案】①②④
【解析】
由题意依次举例对四个命题判断，从而确定答案．
若M＝{x∈Q|x＜0}，N＝{x∈Q|x≥0}，则M没有最大元素，N有一个最小元素0，故①可能成立；
若M＝{x∈Q|x
}，N＝{x∈Q|x
}；则M没有最大元素，N也没有最小元素，故②可能成立；
若M＝{x∈Q|x≤0}，N＝{x∈Q|x＞0}；M有一个最大元素，N没有最小元素，故④可能成立；
M有一个最大元素，N有一个最小元素不可能，因为这样就有一个有理数不存在M和N两个集合中，与M和N的并集是所有的有理数矛盾，故③不可能成立．
故答案为：①②④
【题目】2019年4月，甲乙两校的学生参加了某考试机构举行的大联考，现从这两校参加考试的学生数学成绩在100分及以上的试卷中用系统抽样的方法各抽取了20份试卷，并将这40份试卷的得分制作成如下的茎叶图．
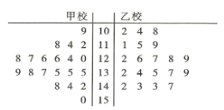
（1）试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数；
（2）若把数学成绩不低于135分的记作数学成绩优秀，根据茎叶图中的数据，判断是否有90
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关；
（3）若从这40名学生中选取数学成绩在
的学生，用分层抽样的方式从甲乙两校中抽取5人，再从这5人中随机抽取3人分析其失分原因，求这3人中恰有2人是乙校学生的概率．
参考公式与临界值表：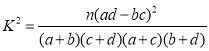
，其中
．
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
