题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]() 分别是棱
分别是棱![]() 上的点(点
上的点(点![]() 不同于点
不同于点![]() ),且
),且![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
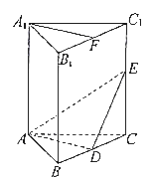
求证:(1)平面![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)推导出BB1⊥AD,AD⊥DE,从而AD⊥平面BCC1B1,由此能证明平面ADE⊥平面BCC1B1.(2)推导出BB1⊥平面A1B1C1,BB1⊥A1F,A1F⊥B1C1,从而A1F⊥平面BCC1B1,再由AD⊥平面BCC1B1,得A1F∥AD,由此能证明A1F∥平面ADE.
(1)在直三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,因为AD平面ABC,所以BB1⊥AD,
又因为AD⊥DE,在平面BCC1B1中,BB1与DE相交,
所以AD⊥平面BCC1B1,
又因为AD平面ADE,所以平面ADE⊥平面BCC1B1.
(2)在直三棱柱ABC﹣A1B1C1中,BB1⊥平面A1B1C1,
因为A1F平面A1B1C1,所以BB1⊥A1F,
又因为A1F⊥B1C1,
在平面BCC1B1中,BB1∩B1C1=B1,
所以A1F⊥平面BCC1B1,
在(1)中已证得AD⊥平面BCC1B1,
所以A1F∥AD,又因为A1F平面ADE,AD![]() 平面ADE,
平面ADE,
所以A1F∥平面ADE.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目